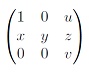Преподаватель: Д.А.Тимашёв

Занятия проходят по понедельникам на 3-й паре (13:15-14:50) в ауд. 450.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 2-е изд., Москва, Факториал, 1995. Дополнительные задачи помечены знаком ★.

Группы, единственность нейтрального и обратного элементов, мультипликативная и аддитивная (для абелевых групп) терминология. Примеры групп: аддитивная и мультипликативная группы кольца, матричные и линейные группы, группы движений, группа диэдра, группы подстановок. Изоморфизм групп, примеры (в т.ч. аддитивная и мультипликативная группы поля R, а также группа положительных вещественных чисел по умножению). Порядок элемента группы, его свойства, циклические группы. Теорема Лагранжа, группы простого порядка. Классификация конечных групп порядка ≤10 (формулировка).

• 5522, 5523, 5607в, 5610, 5615аге, 5626;
• какие из групп изоморфны: аддитивная группа поля рациональных чисел, его мультипликтивная группа, группа положительных рациональных чисел (по умножению)?
• изоморфны ли группы GL_2(C) и GL_3(C)?
• доказать, что любая группа порядка 4 изоморфна либо Z_4 либо V_4;
• ★ доказать, что любая группа порядка 6 изоморфна либо Z_6 либо S_3.

Сопряжённость элементов в группе, классы сопряжённости, центр группы. Вычисление классов сопряженности и центра для групп Q_8, S_n, D_n.

• 5729, 5730б, 5735, 5816б, 5818, 5819агж.

Нормальные подгруппы: три эквивалентных определения. Факторгруппы. Гомоморфизмы, их ядра и образы, каноническая проекция группы на факторгруппу, нормальные подгруппы как ядра гомоморфизмов. Основная теорема о гомоморфизмах групп, вычисление факторгрупп с её помощью.

• 5802, 5803б, 5809а, 5808, 5827аде, 5828где, 5836.

Автоморфизмы групп, группа автоморфизмов Aut(G). Внутренние автоморфизмы, подгруппа внутренних автоморфизмов Inn(G), её нормальность в Aut(G), изоморфизм с G/Z(G). Группа «внешних автоморфизмов» Out(G). Автоморфизмы циклических групп, вычисление Aut(Aut(Aut(Z_9))).

Прямые произведения групп — внутренние и внешние (в аддитивной терминологии — прямые суммы). Разложимость и неразложимость групп в прямое произведение (прямую сумму) на примерах: Z, C, C*, S_3. Разложение конечной циклической группы в прямую сумму примарных циклических подгрупп.

• 5740, 5742★, 5743★, 5838, 6001, 6002бвг, 6005, 6007, 6012;
• можно ли разложить примарную циклическую группу в прямую сумму нетривиальных подгрупп?

Системы порождающих в группах, примеры: циклические группы, S_n, A_n, GL_n. Конечнопорождённые абелевы группы, примеры наличия и отсутствия конечной порождённости (в т.ч. для групп R, Q, Q*). Свободные абелевы группы, базисы и ранг, примеры (группа Z^n свободна, а Z_m — нет). Классификация свободных и конечнопорождённых абелевых групп. Алгоритм вычисления структуры конечнопорождённой абелевой группы, представленной в виде факторгруппы свободной группы, вычисление порядка элемента в факторгруппе.

• 6101а, 6103, 6052агд, 6053, 6051, 6048;
• являются ли конечнопорождёнными следующие группы:
  • аддитивная группа рациональных дробей, знаменатели которых могут делиться только на простые числа из заданного набора p_1,…,p_s;
  • мультипликативная группа ненулевых дробей, у которых числители и знаменатели могут делиться только на p_1,…,p_s?

Вычисление порядка факторгруппы свободной абелевой группы по подгруппе того же ранга. Выражение объёма целочисленного параллелепипеда через количества целых точек внутри параллелепипеда и его граней. Конечные абелевы группы: их классификация по типу разложения на примарные циклические подгруппы, вычисление их факторгрупп, вложимость конечных абелевых групп друг в друга.

• 6039ежз, 6042, 6040ав, 6043а, 6045;
• доказать (с помощью формулы для площади целочисленного параллелограмма) формулу Пика для площади целочисленного многоугольника.

Количество подгрупп данного типа в конечной абелевой группе. Коммутатор элементов в группе, его основное свойство. Коммутант группы, его свойства. Вычисление коммутантов, коммутанты групп S_n, A_n, D_n, GL_n, SL_n. Кратные коммутанты, разрешимость групп. Разрешимость подгрупп и факторгрупп разрешимой группы, критерий разрешимости в терминах подгруппы и факторгруппы. Примеры разрешимых и неразрешимых групп: S_n, D_n, GL_n.

• 6043в, 6207г, 6209, 6220а, 6210, 6213;
• вычислить коммутант группы всех невырожденных вещественных матриц вида
• 
• доказать, что GL_2(Z_2)≅S_3 и GL_2(Z_3)/{±E}≅S_4.

Действия групп на множествах, примеры. Орбиты и стабилизаторы, их свойства. Нахождение орбит и стабилизаторов для некоторых действий. Сопряжённость стабилизаторов точек в одной орбите, связь порядков группы, орбиты и стабилизатора. Порядок группы вращений куба. Действия группы на себе умножениями слева/справа и сопряжениями. Классы сопряжённости и централизаторы, формула классов. p-группы: нетривиальность центра, разрешимость, группы порядка p и p².

• ★ доказать, что группа вращений куба изоморфна S_4;
• 5701бв, 5709бв, 5713★, 5723б, 5731, 5839;
• ★ классифицировать все группы порядка p³.

Силовские подгруппы, теоремы Силова. Когда силовская подгруппа нормальна? Силовские подгруппы в S_3, A_4. Порядок групп GL_n и SL_n над конечным полем. Силовские p-подгруппы в SL_2(Z_p). Силовские подгруппы в прямом произведении групп, пример: силовские 2-подгруппы в D_3×A_4.

• 5904, 5909, 5911, 5913где, 5914, 5915;
• описать все силовские 3-подгруппы в D_3×A_4.

Полупрямые произведения групп (внутренние и внешние), примеры: разложение групп S_n и D_n в полупрямое произведение. Арифметика конечных групп: непростота группы порядка 80, разрешимость групп порядка 20 и 12, коммутативность группы порядка 35, классификация групп порядка pq (p и q — простые числа). Классификация групп порядка ≤10 (кроме порядка 8).

• 5922ав, 5924, 6218вгде★, 6222★, 6223★, 5920вг;
• можно ли разложить группы A_4, Q_8, GL_n(K) в полупрямое произведение?
• ★ перечислить, с точностью до изоморфизма, все группы порядка 8.

Коммутативность группы порядка 455. Линейные и матричные представления групп, примеры: мономиальное представление группы S_n, представление группы в пространстве функций на множестве, определяемое её действием на множестве. Изоморфизм представлений. Инвариантные подпространства. Приводимые, неприводимые и вполне приводимые представления, разложение вполне приводимого представления в прямую сумму неприводимых, примеры: разложение мономиального представления, не вполне приводимое 2-мерное представление группы Z. Теорема Машке.

• 6907, 6909, 6902, 6911, 7018, 7019а.

Неприводимые комплексные представления конечных групп: случай абелевой группы (все неприводимые представления одномерны, описание одномерных представлений, пример: V_4), описание одномерных представлений (примеры: S_n, S_3×D_5), количество и сумма квадратов размерностей неприводимых представлений. Описание неприводимых представлений групп S_3, S_4, и D_n (найдено количество и размерности неприводимых представлений D_n, описаны одномерные представления). Кольца и алгебры. Структурные константы.

• 7002жз, 7010, 7034бге, 7037аб, 6318;
• описать одномерные представления группы A_4×D_4;
• описать неприводимые представления групп A_4 и Q_8.

Алгебра кватернионов H, сопряжение кватернионов, кватернионная норма, H — тело. Задача: классифицировать двумерные алгебры с 1 над C. Идеалы в кольцах и алгебрах. Задача: описать все идеалы в двумерной алгебре с 1, имеющей нильпотентный элемент. Главные идеалы, кольца главных идеалов. Факторкольца и факторалгебры. Изучение факторалгебр алгебры многочленов K[x] над полем K. Присоединение к полю корня неприводимого многочлена. Минимальный многочлен алгебраического элемента в расширении полей.

• 6320б, 6321а, 6408б, 6402а, 6440, 6703бгдеж;
• представить дробь (α^2-3α-1)/(α^2+2α+1), где α∈C удовлетворяет уравнению α^3+α^2+3α+4=0, в виде многочлена от α наименьшей возможной степени (избавиться от иррациональности в знаменателе).

1. Нахождение факторгруппы свободной абелевой группы, вычисление порядка элемента факторгруппы (1 вариант) и количества элементов данного порядка в факторгруппе (2 вариант).
2. Нахождение централизатора подстановки и количества элементов в её классе сопряжённости (1 вариант); описание всех орбит действия заданной матричной группы в векторном пространстве (2 вариант).
3. Доказательство коммутативности группы данного порядка (1 вариант); описание всех силовских подгрупп в данной конечной группе (2 вариант).
4. Нахождение ряда коммутантов заданной матричной группы (1 вариант); доказательство разрешимости группы данного порядка (2 вариант).
5. Описание всех одномерных комплексных представлений заданной конечной группы.
6. Вычисление в факторалгебре алгебры многочленов (1 вариант); избавление от иррациональности в знаменателе дроби в поле, получаемом присоединением корня неприводимого многочлена (2 вариант).