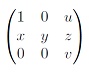Преподаватель: Д.А. Тимашёв

Занятия проходят по пятницам на 3-й паре (13:45-15:20) дистанционно в Zoom.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И. Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.

Группы (напоминание из 1-го семестра): определение, единственность нейтрального и обратного элементов в группе, абелевы группы, мультипликативная и аддитивная терминологии. Примеры групп: аддитивные и мультипликативные группы колец и полей, матричные и линейные группы, группы движений (в т.ч. группа диэдра D_n), группы преобразований множеств (в т.ч. симметрическая группа S_n и знакопеременная группа A_n). Задание конечной группы таблицей умножения, пример: группа Клейна V_4. Изоморфизм групп, примеры изоморфных и неизоморфных групп: аддитивная и мультипликативная группы поля R, а также группа положительных вещественных чисел по умножению; Z_6, S_3 и D_3; Z_4 и V_4. Порядок элемента группы.

• 55.25абг, 55.26, 56.9, 56.10, 56.11;
• доказать, что множество G с ассоциативной операцией, в котором есть правая единица (элемент e со свойством g·e=g, ∀g∈G) и правый обратный для каждого g∈G (элемент g' со свойством g·g'=e), является группой;
• какие из групп изоморфны: аддитивная группа поля рациональных чисел, его мультипликтивная группа, группа положительных рациональных чисел (по умножению)?
• изоморфны ли группы GL_2(C) и GL_3(C)?

Сопряжённость элементов в группе, классы сопряжённости, центр группы. Совпадение порядков сопряжённых элементов. Вычисление классов сопряженности и центра для групп S_n и D_n. Циклические группы. Теорема Лагранжа и её следствия. Группы простого порядка.

• 56.7бв, 56.28, 57.30б, 58.11бв, 58.19б, 58.22;
• доказать, что любая группа порядка 4 изоморфна либо Z_4 либо V_4;
• ★ доказать, что любая группа порядка 6 изоморфна либо Z_6 либо S_3.

Классификация конечных групп порядка ≤10 (не всё доказано). Нормальные подгруппы: эквивалентные определения, примеры. Нормальные подгруппы в группах S_3 и S_4.

• 58.3, 58.4б, 58.10, 58.11а.

Факторгруппы. Гомоморфизмы, ядро и образ, связь с нормальными подгруппами. Основная теорема о гомоморфизмах, её применение к вычислению факторгрупп. Автоморфизмы групп, автоморфизмы циклических групп, внутренние автоморфизмы.

• 58.31аде, 58.32агд, 58.42, 57.40, 57.41, 57.42;
• ★ доказать, что Aut(S_n)=Inn(S_n)≅S_n, кроме случаев n=2,6.

Прямое произведение (прямая сумма) групп, примеры разложений и неразложимости групп в прямые произведения (прямые суммы). Полупрямое произведение групп, примеры.

• 60.2бвг, 60.5, 60.7, 60.8, 60.12;
• какие из групп в задаче 60.2 разложимы (нетривиальным образом) в полупрямое произведение?
• как устроен гомоморфизм Z_2 → Aut Z_n, задающий разложение группы D_n в полупрямое произведение Z_n и Z_2?
• разложить в полупрямое произведение группы: а) GL_n(K) б) невырожденных верхнетреугольных матриц размера n×n.

Системы порождающих в группах. Конечнопорождённые абелевы группы, примеры наличия и отсутствия конечной порождённости (в т.ч. для групп Z_m, R, Q, Q*). Свободные абелевы группы, базисы и ранг, примеры (группа Z^n свободна, а Z_m — нет). Классификация свободных и конечнопорождённых абелевых групп. Алгоритм вычисления структуры конечнопорождённой абелевой группы, представленной в виде факторгруппы свободной группы.

Видеозапись семинара

• 60.48, 60.51, 60.52агд, 60.53;
• являются ли конечнопорождёнными следующие группы:
  • аддитивная группа рациональных дробей, знаменатели которых могут делиться только на простые числа из заданного набора p_1,…,p_s;
  • мультипликативная группа ненулевых дробей, у которых числители и знаменатели могут делиться только на p_1,…,p_s?

Вычисление порядка элемента в конечно порождённой абелевой группе, представленной как факторгруппа свободной группы. Критерий конечности факторгруппы свободной абелевой группы. Конечные абелевы группы, их структура, тип группы. Классификация конечных абелевых групп заданного порядка. Вложимость конечных абелевых групп друг в друга.

• 60.39ежз, 60.40ав, 60.45, 60.54;
• доказать две формулы для объёма целочисленного n-мерного параллелепипеда П:
  1. vol(П) = число целых точек в П, не лежащих на его гранях, не содержащих данную вершину 0;
  2. vol(П) = ∑ (1/2^k)⋅(число целых точек внутри всех (n-k)-мерных граней П), где суммирование ведётся по k=0,1,…,n;
• доказать формулу Пика для площади целочисленного многоугольника P:
• S(P) = (число целых точек внутри P)+½⋅(число целых точек на периметре P)-1.

Определение типа факторгруппы конечной абелевой группы. Количество подгрупп заданного порядка в данной конечной абелевой группе. Действия групп на множествах, описание орбит.

• 60.42, 60.43бв, 57.1бв, 57.2, 57.3.

Вычисление стабилизаторов. Стабилизаторы точек в одной орбите. Связь порядков группы, орбиты и стабилизатора. Пять правильных многогранников, двойственность между ними. Группы движений двойственных многогранников совпадают. Группы вращений и движений куба. Действие группы на себе сопряжениями: классы сопряжённости и централизаторы, число элементов в классе сопряжённости, формула классов. Нетривиальность центра конечной p-группы, группы порядка p^2 (p — простое число).

• 57.9бв, 57.12в, 57.14б, 57.23б, 57.25, 57.31, 58.43;
• найти группы вращений и движений тетраэдра;
• ★ найти группы вращений и движений икосаэдра;
• ★ перечислить с точностью до изоморфизма все группы порядка p^3.

Коммутант группы, его свойства. Вычисление коммутанта группы G методом оценки сверху (ядро гомоморфизма G в абелеву группу) и снизу (подгруппа, порождённая некоторым количеством коммутаторов). Кратные коммутанты, разрешимые группы, критерий разрешимости (в терминах подгруппы и факторгруппы).

• 62.7г, 62.8б, 62.19, 62.20, 58.37;
• доказать, что -E не является коммутатором в группе SL_2(R);
• доказать, что GL_2(Z_2) ≅ S_3;
• найти коммутант группы, состоящей из невырожденных действительных матриц вида
• 

Силовские подгруппы, теоремы Силова, примеры: силовские подгруппы в A_4, в GL_2(Z_p), в прямом произведении групп. Арифметика конечных групп: доказательство непростоты и разрешимости групп заданного порядка.

• 59.3а, 59.4а, 59.13где, 59.15, 59.22ав, 59.24, 62.18вгде★;
• описать все силовские подгруппы в D_3×A_4.

Арифметика конечных групп: доказательство коммутативности групп заданного порядка.

Линейные и матричные представления групп, в том числе представление в пространстве функций на множестве с действием группы. Приводимые и вполне приводимые представления, разложение в прямую сумму неприводимых представлений. Нахождение инвариантных подпространств и доказательство неприводимости (пример: мономиальное представление группы S_n).

• 59.20вг, 69.7, 69.9, 69.11;
• разложить мономиальное представление группы A_n над полем C на неприводимые слагаемые.

Теорема Машке. Описание неприводимых комплексных представлений конечных абелевых групп (пример: V_4) и одномерных комплексных представлений конечных групп (пример: S_3×D_5). Факты о количестве и размерностях неприводимых комплексных представлений конечной группы. Описание всех неприводимых комплексных представлений группы D_n размерности >1.

• 69.2, 70.2жз, 70.10, 70.34бге, 70.37аб;
• описать все одномерные комплексные представления групп D_n и A_4×D_4.
• описать все неприводимые комплексные представления групп A_4 и Q_8.

Кольца и алгебры, примеры. Структурные константы. Классификация двумерных комплексных алгебр с единицей. Идеалы. Факторалгебры K[x]/(f), их свойства, вычисления в K[x]/(f), присоединение корня.

• 63.21б, 63.22а, 64.8б, 64.42, 67.3бгдеж, 67.12★;
• представить выражение (a²-3a-1)/(a²+2a+1) в виде многочлена от a наименьшей возможной степени с рациональными коэффициентами, где a∈C — корень многочлена x³+x²+3x+4;
• в поле F_16, полученном из Z_2 присоединением корня a неприводимого многочлена x^4+x+1, найти порядок элемента a²+a в мультипликативной группе поля и его минимальный многочлен над Z_2.

1. Вычисление факторгруппы свободной абелевой группы и нахождение в ней количества элементов заданного порядка (1 и 4 варианты) и порядка заданного элемента (2 и 3 варианты).
2. Нахождение централизатора элемента группы подстановок и количества элементов в его классе сопряжённости (1 и 3 варианты); описание орбит действия группы на множестве (2 и 4 варианты).
3. Доказательство коммутативности группы заданного порядка (1 и 3 варианты); описание силовских подгрупп в группе (2 и 4 варианты).
4. Вычисление производного ряда группы (1 и 3 варианты); доказательство разрешимости группы заданного порядка (2 и 4 варианты).
5. Описание одномерных комплексных представлений группы.
6. Избавление от иррациональности в знаменателе выражения в поле, получаемом присоединением корня неприводимого многочлена к полю Z_2 (1 вариант), Z_3 (3 вариант) и C (2 и 4 варианты).