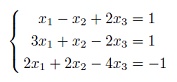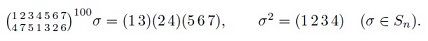Преподаватель: Д.А.Тимашёв

Занятия проходят по понедельникам c 18:30 по 21:50 в ауд. 405.

1. Системы линейных уравнений, методы их решения.
2. Векторные пространства, линейная зависимость векторов, базис. Ранг системы векторов и размерность пространства.
3. Матрицы, операции над ними (матричная алгебра).
4. Перестановки и подстановки.
5. Определители.
6. Основные алгебраические структуры: группы, кольца, поля.
7. Комплексные числа, «основная теорема алгебры».
8. Вычеты.
9. Теория многочленов: деление с остатком, корни многочленов, разложение на множители.
10. Многочлены от нескольких переменных. Симметрические многочлены.
11. Рациональные дроби.

1. А.И.Кострикин. Введение в алгебру. Часть I. Основы алгебры.
2. Э.Б.Винберг. Курс алгебры.
3. А.Г.Курош. Курс высшей алгебры.
4. Сборник задач по алгебре под ред. А.И.Кострикина. Часть I. Основы алгебры.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.

Системы линейных уравнений (СЛУ) и их решения: определение и примеры. Совместные и несовместные, определённые и неопределённые СЛУ. Матрица коэффициентов и расширенная матрица системы.

Элементарные преобразования систем линейных уравнений и их матриц. Элементарное преобразование приводит к эквивалентной СЛУ.

Метод Гаусса решения СЛУ: ведущие элементы (лидеры) строк матрицы, приведение к ступенчатому и улучшенному ступенчатому виду, ранг ступенчатой матрицы, анализ ступенчатой СЛУ, главные и свободные неизвестные, общее решение системы. Критерий совместности и определённости СЛУ в терминах рангов ступенчатых матриц. Преимущество улучшенного ступенчатого вида.

Однородные системы линейных уравнений (ОСЛУ), их совместность. ОСЛУ с числом уравнений меньше числа неизвестных имеет ненулевое решение.

Решение систем линейных уравнений методом Гаусса (8.1а, 8.2а). Связь решений совместной СЛУ и ассоциированной ОСЛУ. Квадратные СЛУ, критерий определённости: ассоциированная ОСЛУ должна быть определена. Полиномиальная интерполяция.

• 8.1вг, 8.2вд, 8.8;
• закончить доказательство теоремы о полиномиальной интерполяции;
• ★ найти явную формулу для интерполяционного многочлена.

Векторные пространства: определение, простейшие следствия аксиом, примеры — геометрические векторы, арифметическое пространство R^n, пространство функций на множестве.

Линейные комбинации векторов, их значения, тривиальная комбинация. Линейная зависимость, примеры (случай одного и двух векторов). Свойства линейной зависимости. Обобщение на бесконечные системы векторов. Основная лемма о линейной зависимости.

Эквивалентность условий максимальности линейно независимой подсистемы в системе векторов и выражаемости остальных векторов системы через эту подсистему. Базис системы векторов: определение, примеры — базисы в пространстве геометрических векторов, стандартный базис в R^n. Координаты вектора в базисе, пример: координаты в стандартном базисе пространства R^n.

Любая система векторов в R^n имеет базис, и во всех базисах одинаковое число векторов (≤n). Ранг системы векторов и размерность векторного пространства.

Метод Крамера решения квадратных систем линейных уравнений размеров 2×2 и 3×3 (8.6бг). Определители 2-го и 3-го порядка.

• 8.6вд, 8.2е, 9.1г, 9.2ж, 16.1★;
• решить методом Крамера систему линейных уравнений:
• 

Ранг матрицы: горизонтальный, вертикальный и ступенчатый ранги, их совпадение. Свойства: ранг матрицы не превосходит любого из её размеров, не меняется при элементарных преобразованиях строк и столбцов и при транспонировании.

Теорема Кронекера–Капелли. Критерий определённости СЛУ в терминах рангов.

Подпространства в векторных пространствах. Линейная оболочка системы векторов.

Пространство решений ОСЛУ, его размерность. Фундаментальная система решений (ФСР) однородной системы, метод её построения по улучшенному ступенчатому виду матрицы коэффициентов. Структура множества решений произвольной совместной СЛУ как сдвига подпространства решений ассоциированной ОСЛУ на вектор частного решения, геометрический смысл.

Алгоритм нахождения базиса системы векторов и выражения остальных векторов через базис (6.12а). Нахождение ФСР и размерности пространства решений ОСЛУ (8.4а). Вычисление ранга матрицы (7.2ж).

• 6.12ви, 6.13, 8.4вг, 7.2аз, 7.6, 7.19★.

Линейные отображения: определение, задание линейных отображений арифметических пространств матрицами, интерпретация СЛУ на языке линейных отображений. Операции над линейными отображениями и матрицами: сложение, умножение на числа, умножение. Матричная запись линейных отображений и систем линейных уравнений.

Алгебраические свойства матричных операций, матричные операции и транспонирование. Теорема о ранге произведения матриц.

Единичная матрица, её основное свойство. Обратная матрица, её единственность. Произведение обратимых матриц обратимо.

Невырожденные матрицы. Квадратная матрица обратима тогда и только тогда, когда она невырождена. Алгоритм вычисления обратной матрицы.

Умножение матриц (17.1г), возведение в степень (17.4б). Пример некоммутирующих квадратных матриц. Матричные единицы — стандартный базис пространства матриц.

• 17.1бв, 17.4ав, 17.13, 17.25.

Элементарные матрицы, их основное свойство. Обратимость элементарных матриц. Разложение произвольной невырожденной матрицы в произведение элементарных матриц.

Перестановки, их количество. Подстановки степени n, их двухрядная запись. Взаимно однозначное соответствие между перестановками и подстановками, количество подстановок степени n равно n!.

Умножение подстановок, его свойства. Тождественная подстановка и подстановка, обратная к данной.

Циклические подстановки (циклы), их орбиты, однорядная запись цикла. Независимость циклов, разложение произвольной подстановки в произведение независимых циклов, его единственность.

Транспозиции, разложение произвольной подстановки в произведение транспозиций.

Матричные уравнения вида AX=B, метод их решения. Вычисление обратной матрицы (18.9е). Умножение подстановок (3.1а), разложение подстановки в произведение независимых циклов (3.2а), возведение подстановок в степень. Решение уравнений в подстановках.

• 18.3взи, 18.9кл, 3.1вг, 3.2бе;
• решить уравнения в подстановках:
• 

Инверсии в перестановке, чётность и знак перестановки и подстановки. Изменение чётности перестановки при транспозиции двух элементов. Количество чётных и нечётных перестановок n элементов (или подстановок степени n) одинаково и равно n!/2. Определение знака подстановки по числу сомножителей в её разложении на транспозиции. Знак произведения подстановок. Знак обратной подстановки.

Определители квадратных матриц: определение по развёрнутой формуле. Свойства определителя как функции от набора строк матрицы: аддитивность и однородность (вместе — полилинейность), кососимметричность, определитель матрицы с нулевой строкой, с одинаковыми и с пропорциональными строками, неизменность при элементарных преобразованиях 1-го типа.

Определитель транспонированной матрицы, свойства определителя как функции от набора столбцов.

Определитель треугольной матрицы. Метод вычисления определителя приведением матрицы к треугольному виду. Квадратная матрица невырождена тогда и только тогда, когда её определитель не равен 0.

Определение чётности и знака подстановки (3.6а). Игра «15»: можно ли переставить местами фишки 14 и 15, сохранив расположение остальных фишек?

Вычисление определителей размеров 4×4 (13.1б) и n×n (13.2д) приведением к треугольному виду.

• 3.6бж, 13.1вж, 13.2аж;
• можно ли поворотами слоёв кубика Рубика на шарнирах добиться того, чтобы угловые кубики одной из его граней переставились по циклу, а остальные кубики остались на своих местах (возможно, повернувшись)?

Определитель матрицы с углом нулей. Определитель Вандермонда, его основное свойство. Определитель произведения матриц.

Миноры прямоугольной матрицы. Дополнительный минор и алгебраическое дополнение к элементу квадратной матрицы. Разложение определителя по строке и по столбцу, фальшивое разложение.

Присоединённая матрица, её основное свойство. Формула для обратной матрицы. Пример: формула для обратной к матрице размера 2×2.

Правило Крамера для решения квадратных СЛУ.

Теорема о ранге матрицы (его совпадение с наибольшим порядком ненулевого минора), метод окаймляющих миноров для вычисления ранга матрицы.

Вычисление определителей: сведение к определителю Вандермонда (14.1и), определитель произведения матриц (15.2аг).

• 14.1км, 15.2в, 16.19.

Группы: определение, единственность нейтрального и обратного элемента, примеры групп. Абелевы группы. Сравнение мультипликативной и аддитивной терминологий в теории групп. Подгруппы: определение и примеры.

Кольца: определение, аддитивная группа кольца. Классы колец: ассоциативные, коммутативные, кольца с единицей. Примеры колец.

Обратимые элементы в ассоциативных кольцах с единицей, примеры: 1 обратима, 0 не обратим в кольцах с числом элементов >1. Мультипликативная группа кольца, примеры.

Делители нуля, их необратимость. Возможность сокращения на множитель, не являющийся делителем нуля.

Поля: определение и примеры. Перенос теории линейных уравнений, векторов, матриц и определителей с поля R на произвольное поле. Подкольца и подполя: определение и примеры.

Сравнимость целых чисел по модулю m, классы вычетов. Операции над вычетами, их корректность. Кольцо вычетов Z_m.

Вычисление определителей разложением по строке/столбцу (12.3а) и с использованием рекуррентных уравнений (14.1а). Формула для обратной матрицы (18.8ви). Вычисление ранга матрицы методом окаймления миноров (7.1а).

• 12.1, 12.3дз, 14.1б, 18.8гк, 7.1дл.

Делители нуля и обратимые элементы в кольцах вычетов. Z_m — поле тогда и только тогда, когда m — простое число.

Характеристика поля, примеры. Если характеристика поля положительна, то это простое число. Возведение суммы в степень, равную характеристике поля. Малая теорема Ферма.

Комплексные числа: аксиоматическое определение поля C, алгебраическая форма записи комплексных чисел, построение поля C. Изоморфизм групп, колец и полей. Единственность поля комплексных чисел с точностью до изоморфизма.

Решение систем линейных уравнений над полями вычетов (66.19). Решение квадратных уравнений над полем вычетов (66.24аб) и извлечение корней (66.23б). Вычисления над комплексными числами в алгебраической форме (20.1г).

• 66.20, 8.10б, 66.24вг, 66.23в, 66.32, 20.1еж.

Геометрическая интерпретация комплексных чисел как точек или векторов на координатной плоскости. Геометрический смысл операций сложения и вычитания комплексных чисел. Модуль комплексного числа и сопряжённое число, их геометрический смысл, свойства операции сопряжения. Деление комплексных чисел в алгебраической форме.

Аргумент комплексного числа, его главная ветвь. Тригонометрическая форма записи комплексных чисел. Свойства модуля и аргумента, формула Муавра. Умножение и деление комплексных чисел в тригонометрической форме, геометрический смысл этих операций. Экспоненциальный вариант тригонометрической формы записи комплексных чисел.

Извлечение корней из комплексных чисел. Корни из единицы, первообразные корни.

Доказательство геометрических теорем методами алгебры комплексных чисел (сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон). Вычисления над комплексными числами в тригонометрической форме (21.2е). Выражение тригонометрических функций кратных углов с помощью комплексных чисел (21.11вг). Извлечение корней из комплексных чисел (22.7гдм). Вычисление сумм с помощью комплексных чисел (23.1аб).

• 21.2бж, 21.12, 22.7ипр, 23.1вг, 23.2аг;
• ★ доказать с помощью комплексных чисел теорему Птолемея: произведение диагоналей четырёхугольника, вписанного в окружность, равно сумме произведений его противоположных сторон.

Многочлены: аксиоматическое определение кольца многочленов K[x] от одной переменной над полем K, его существование и единственность с точностью до изоморфизма. Степень многочлена, её свойства. Отсутствие делителей нуля и обратимые элементы в кольце K[x].

Деление с остатком в кольце многочленов. Теорема Безу. Корни многочленов, кратность корня, простые и кратные корни. Число корней многочлена, с учётом их кратностей, не превосходит его степени.

Производная многочлена, её свойства. Высшие производные. Связь кратности корня со значениями производных.

Разложение многочлена по степеням линейного двучлена. Формула Тейлора.

Вычисление тригонометрических сумм с помощью комплексных чисел (23.2а). Схема Горнера (26.1г). Разложение многочлена по степеням линейного двучлена и вычисление значений его производных (26.2а).

• 26.1б, 26.2б, 26.3бв, 26.5, 26.7аб, 26.11★.

Наибольший общий делитель (НОД) двух многочленов, его существование и единственность с точностью до умножения на константу. Алгоритм Евклида для нахождения НОД. Линейное выражение НОД через исходные многочлены.

Неприводимые многочлены, существование и единственность разложения многочлена на неприводимые множители. Выяснение делимости многочленов друг на друга, нахождение их НОД и НОК в терминах разложения на неприводимые множители.

Основная теорема алгебры комплексных чисел: любой многочлен положительной степени над полем C имеет комплексный корень. Её следствия: неприводимые многочлены над полем C — это многочлены 1-й степени, разложение многочлена над полем C на линейные множители, число комплексных корней многочлена, с учётом кратностей, равно степени многочлена.

Определение кратности корня многочлена (26.3а). Связь кратности корня со значениями производных (26.5, 26.7а). Вычисление НОД многочленов по алгоритму Евклида (25.2а). Линеное выражение для НОД: (f,g)=uf+vg, с ограничениями на степени u и v, его единственность и нахождение методом неопределённых коэффициентов (25.3а).

• 25.2вг, 25.3б;
• найти НОД многочленов x^m-1 и x^n-1.

Комплексные корни многочлена с действительными коэффициентами, их разбиение на пары сопряжённых друг другу корней одинаковой кратности. Разложение многочлена над неприводимые множители (линейные и квадратичные с отрицательным дискриминантом) над полем R.

Поле дробей ассоциативного коммутативного кольца с 1 без делителей нуля. Поле рациональных дробей K(x). Интерпретация рациональных дробей как функций.

Несократимые дроби. Представление элемента поля K(x) несократимой дробью, его единственность.

Правильные дроби. Представление рациональной дроби в виде суммы многочлена и правильной дроби, его единственность.

Простейшие дроби, их описание над полями C и R. Разложение правильной дроби в сумму простейших дробей.

Разложение на неприводимые множители над полем C (27.1г). Делимость многочленов над C и комплексные корни (27.5). Разложение на неприводимые множители над полем R (27.2а). Рациональные корни многочленов над полем Q (28.2а).

• 27.1б, 27.7, 27.2бге, 28.2бв, 28.1в.

Кольцо K[x_1,…,x_n] многочленов от нескольких переменных над ассоциативным коммутативным кольцом K с единицей: аксиоматическое определение, существование и единственность с точностью до изоморфизма. Степень одночлена и многочлена, однородные многочлены, разложение многочлена в сумму однородных компонент.

Лексикографический порядок на одночленах, его свойства. Старший член ненулевого многочлена. Старший член произведения многочленов, отсутствие делителей нуля в кольце K[x_1,…,x_n] многочленов над кольцом K без делителей нуля.

Симметрические многочлены: определение и примеры. Степенные суммы и элементарные симметрические многочлены.

Теорема Виета: выражение значений элементарных симметрических многочленов на корнях многочлена от одной переменной через его коэффициенты.

Основная теорема о симметрических многочленах: существование и единственность выражения произвольного симметрического многочлена через элементарные симметрические многочлены.

Разложение рациональной дроби в сумму простейших дробей над полями C (29.1ж) и R (29.2в). Выражение симметрического многочлена через элементарные методом неопределённых коэффициентов (пример: выражение s_3=x_1^3+…+x_n^3; задача: выразить s_4=x_1^4+…+x_n^4).

• 29.1бе, 29.2аги, 31.9авер, 31.15★, 31.2, 31.5.

Выражение значения симметрического многочлена на корнях многочлена от одной переменной через его коэффициенты. Дискриминант многочлена от одной переменной, его основное свойство: дискриминант равен 0 тогда и только тогда, когда многочлен имеет кратные корни. Дискриминант квадратного и приведённого кубического трёхчленов.

Сумма квадратов и произведение всех корней многочлена (31.2а). Решение симметрической системы алгебраических уравнений (31.21а). Выяснение наличия кратных корней у многочлена с помощью дискриминанта (32.8а).

• 31.21б, 31.26а, 32.8б.

9 января, 10:00, ауд. 405.

8 января, 10:00, ауд. 407.

Программа экзамена