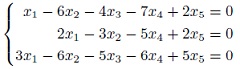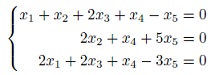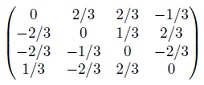Преподаватель: Д.А.Тимашёв

Лекции читаются по понедельникам на 2-й паре (10:45-12:20) и по средам на 1-й паре (9:00-10:35) еженедельно а ауд. 14-13.

Семинары проходят по понедельникам на 3-й паре (13:15-14:50) и по средам на 2-й паре (10:45-12:20) еженедельно а ауд. 14-13.

• 27 мая 2022, 9:00−13:00, ауд. 14-13
• 30 мая 2022, 10:00−14:00, ауд. 14-13
• 3 июня 2022, 10:00−14:00, ауд. 14-13

• 16 июня 2022, 10:00, ауд. 14-13

• 15 июня 2022, 15:00, ауд. 13-03

Программа экзамена

1. Э.Б.Винберг. Курс алгебры. Главы 5−8.
2. А.И.Кострикин, Ю.И.Манин. Линейная алгебра и геометрия.
3. А.И.Кострикин. Введение в алгебру. Часть II. Линейная алгебра.
4. Сборник задач по алгебре под ред. А.И.Кострикина. Часть II. Линейная алгебра и геометрия.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, Москва, МЦНМО, 2009. Дополнительные задачи помечены знаком ★.

Векторные пространства над произвольным полем K, скаляры и векторы, примеры: геометрические векторы, арифметическое пространство K^n, пространство матриц, пространство функций на множестве, пространство многочленов, расширения полей. Простейшие следствия аксиом векторного пространства.

Линейные комбинации векторов, линейная зависимость, основная лемма о линейной зависимости.

Базис и размерность векторного пространства, координаты вектора в базисе. Конечномерные и бесконечномерные векторные пространства.

Изоморфизм векторных пространств. Любое векторное пространство размерности n<∞ над полем K изоморфно арифметическому пространству K^n.

Видеозапись лекции

Примеры векторных пространств. Аддитивную группу Z нельзя превратить в векторное пространство. Линейная независимость систем функций на вещественной прямой. Расширения полей, число элементов конечного поля.

• 34.3дж, 34.4б, 34.5, 34.7вг, 34.8д★з, 35.10абвг;
• доказать, что множество R^+ положительных чисел с операциями x⊕y = x·y (x,y∈R^+) и λ⊗x = x^λ (λ∈R, x∈R^+) является векторным пространством над полем R, и найти его размерность.

Матрица перехода от одного базиса к другому, её свойства. Правило преобразования координат вектора при замене базиса.

Подпространства в векторном пространстве, примеры и конструкции подпространств: линейная оболочка множества векторов, пространство решений однородной системы линейных уравнений, пересечение подпространств. Объединение подпространств — вообще говоря, не подпространство. Сумма подпространств.

Подпространство конечномерного векторного пространства конечномерно, его размерность не превосходит размерности пространства и строго меньше для собственного подпространства. Базис пространства, согласованный с подпространством. Существование базиса конечномерного пространства, согласованного с парой подпространств, их суммой и пересечением. Формула Грассмана для размерности суммы двух подпространств. Нетривиальность пересечения двух подпространств, сумма размерностей которых больше размерности пространства.

Видеозапись лекции

Преобразование координат вектора при замене базиса. Примеры подпостранств. Количество подпространств данной размерности в векторном пространстве над конечным полем. Применения формулы Грассмана. Взаминое расположение подпространств в конечномерном векторном пространстве, инварианты конфигураций подпространств.

• 34.10в, 34.11а, 34.12, 35.3вдеж, 35.10е;
• если матрица A размера n×n имеет ранг ≤n/2, то матричное уравнение AX=0 имеет решением ненулевую симметрическую матрицу X;
• какими инвариантами задаётся конфигурация трёх подпространств в конечномерном пространстве с точностью до эквивалентности?
• для задания четвёрки подпространств с точностью до эквивалентности недостаточно дискретных инвариантов (размерностей самих подпространств, их сумм, пересечений, …).

Факторпространство векторного пространства по подпространству: определение и примеры. Размерность факторпространства, коразмерность подпространства.

Линейная независимость подпространств, (внутренняя) прямая сумма подпространств, проекции вектора на прямые слагаемые, примеры. Внешняя прямая сумма векторных пространств, её связь с внутренней прямой суммой. Размерность и базис прямой суммы подпространств.

Видеозапись лекции

Двойное отношение четвёрки прямых на плоскости. Когда объединение двух подпространств является подпространством? Линейная независимость подпространств (недостаточность тривиальности их попарных пересечений), прямые суммы, проекции на слагаемые.

• 35.13аб, 35.17а, 35.19, 35.22б, 35.23, 35.24, 35.25, 35.27.

Дополнение к подпространству в конечномерном векторном пространстве. Факторизация прямой суммы подпространств по слагаемым.

Линейные функции на векторном пространстве V: определение, примеры (след матрицы, вычисление значения функции в точке множества), запись в координатах на конечномерном пространстве (линейные формы). Сопряжённое (двойственное, дуальное) пространство V*, его размерность. Сопряжённый (двойственный, дуальный) базис пространства V*. Канонический изоморфизм пространств V и (V*)* в конечномерном случае. Двойственность между векторами и линейными функциями (ковекторами).

Аннулятор подмножества в векторном пространстве, его свойства. Размерность аннулятора, совпадение второго аннулятора подпространства с этим подпространством в конечномерном случае. Задание подпространства в конечномерном векторном пространстве однородной системой линейных уравнений (ОСЛУ). Критерий базисности набора линейных функций: задаваемая ими квадратная ОСЛУ имеет только нулевое решение.

Видеозапись лекции

Ядро линейной функции. Интерполяционная формула Лагранжа как разложение многочлена по базису в терминах сопряжённого базиса. Задание подпространства однородной системой линейных уравнений ⇔ нахождение аннулятора подпространства.

• 35.16б, 36.9в, 36.14, 36.16, 36.17бв, 36.18★;
• доказать, что набор линейных функций (β_0,…,β_n) на пространстве V многочленов степени ≤n над полем K зарактеристики 0, где β_i(f) равно значению i-й производной многочлена f в точке t_0∈K, образует базис пространства V*, найти сопряжённый ему базис в пространстве V и разложение произвольного многочлена f∈V по этому базису;
• (кратная интерполяция) доказать, что для любого набора попарно различных точек x_1,…,x_k на действительной прямой, любого набора натуральных чисел n_1,…,n_k и любого набора значений y_ij (1≤i≤k, 0≤j<n_i) существует единственный многочлен f степени < n_1+…+n_k, у которого значение j-й производной в точке x_i равно y_ij (при всех возможных i,j);
• для произвольного подпространства U в конечномерном векторном пространстве V построить канонические изоморфизмы U* ≅ V*/U° и (V/U)* ≅ U°.

Линейные отображения векторных пространств: определение, примеры (изоморфизмы, линейные функции, поворот плоскости, проекция пространства на плоскость, проекции на слагаемые в прямой сумме, факторизация по подпространству, дифференцирование функций). Матрица линейного отображения: определение, примеры (матрицы поворота плоскости и проекции пространства на плоскость), запись линейного отображения в координатах. Взаимно однозначное соответствие между линейными отображениями и матрицами (при выборе базисов). Преобразование матрицы линейного отображения при замене базисов. Операции над линейными отображениями и соответствующие операции над матрицами (сложение, умножение на скаляр, произведение).

Ядро и образ линейного отображения. Размерность образа, ранг линейного отображения. Критерии инъективности/сюръективности/биективности линейного отображения в терминах ядра и образа.

Видеозапись лекции

Нахождение базиса и системы линейных уравнений для суммы и пересечения подпространств.

• 35.15в, 36.2, 36.3, 36.4;
• найти ОСЛУ для суммы подпространств U,W в 5-мерном векторном пространстве V, которые заданы с помощью ОСЛУ:
• и

Изоморфизм V/Ker(A) ≅ Im(A) для линейного отображения A пространства V, (ко)размерность ядра и образа. Геометрическая структура линейного отображения: подпространство, дополнительное к ядру, изоморфно отображается на образ. Геометрическая интерпретация систем линейных уравнений (СЛУ) в терминах линейных отображений, новые доказательства теорем о связи множеств решений СЛУ и ассоциированной ОСЛУ и размерности пространства решений ОСЛУ.

Сопряжённое линейное отображение и его свойства: взаимодействие операции сопряжения с другими операциями на линейных отображениях, матрица сопряжённого отображения, его ядро и образ.

Линейные операторы на векторном пространстве (пример: единичный оператор). Матрица линейного оператора, её преобразование при замене базиса. Алгебра линейных операторов, её изоморфизм с алгеброй квадратных матриц.

Определитель и след линейного оператора, их независимость от выбора базиса. Невырожденные линейные операторы, эквивалентные условия невырожденности. Полная и специальная линейные группы.

Видеозапись лекции

Связь свойств инъективности и сюръективности сопряжённых друг другу линейных отображений. Квазиобратная матрица. Нахождение матрицы линейного оператора, её преобразование при замене базиса.

• 36.1, 39.13★, 39.15гзн, 39.20, 39.21, 39.23;
• доказать, что для любых матриц A и B размеров m×n и n×m из равенств AB=E и BA=E вытекает, что m=n;
• доказать, что Im(A*) ≅ (Im A)*, и вывести из этого, что ранг матрицы A по строкам равен её рангу по столбцам.

Инвариантные подпространства для линейного оператора, вид матрицы оператора в базисе, согласованном с инвариантными подпространствами.

Собственные векторы и собственные значения линейного оператора. Характеристический многочлен. Наличие собственных векторов у линейного оператора в векторном пространстве над алгебраически замкнутым полем. Собственные подпространства, их линейная независимость. Алгебраическая и геометрическая кратности собственного значения. Диагонализуемые операторы, эквивалентные условия диагонализуемости. Операторы с простым спектром диагонализуемы. Проекторы.

Видеозапись лекции

Инвариантные подпространства оператора дифференцирования на пространстве многочленов. Вычисление коэффициентов характеристического многочлена. Вычисление собственных значений и нахождение собственных векторов. Диагонализумость линейных операторов.

• 40.7, 40.9, 40.15вде, 40.16ав, 40.24, 40.25, 40.44★;
• ★ доказать, что любой многочлен со старшим коэффициентом 1 является характеристическим многочленом некоторого линейного оператора;
• доказать, что линейный оператор R со свойством R²=E диагонализуем с собственными значениями 1 и -1 (такие линейные операторы называются отражениями).

Корневые векторы линейного оператора (пример: собственные и корневые векторы оператора дифференцирования в пространстве функций на прямой). Корневые подпространства, их свойства: инвариантность, размерность равна алгебраической кратности собственного значения, ограничение оператора на корневое подпространство. Линейная независимость корневых подпространств, разложение векторного пространства в прямую сумму корневых подпространств.

Видеозапись лекции

Коммутирующие семейства линейных операторов. Нахождение корневых подпространств. Корневое разложение инвариантного подпространства.

• 40.27, 40.29, 40.33, 40.35бг, 40.38;
• доказать, что для любого семейства коммутирующих диагонализуемых линейных операторов существует базис, в котором матрицы всех этих операторов диагональны.

Циклические подпространства для нильпотентного линейного оператора, их свойства: инвариантность, базис и размерность, матрица нильпотентного оператора на циклическом подпространстве — нильпотентная жорданова клетка. Разложение векторного пространства в прямую сумму циклических подпространств, жорданов базис и жорданова нормальная форма для нильпотентного оператора. Графическое изображение действия нильпотентного оператора на жордановом базисе с помощью диаграммы Юнга.

Жорданова нормальная форма (ЖНФ) и жорданов базис (ЖБ) для линейного оператора в конечномерном векторном пространстве над алгебраически замкнутым полем: формулировка теоремы. Формулы для количества жордановых клеток с заданным собственным значением (всех и данного размера) в ЖНФ.

Видеозапись лекции

Нахождение ЖНФ и ЖБ.

• 41.1жклм, 41.5, 41.7, 41.10бвг, 41.17.

Доказательство теоремы о ЖНФ линейного оператора. Комплексификация вещественных векторных пространств и вещественных линейных операторов.

Видеозапись лекции

Приложения ЖНФ: критерий нильпотентности в терминах собственных значений, вычисление циркулянта, оценка снизу размерности централизатора матрицы.

• 41.9, 41.14★, 41.15, 41.18, 41.20, 41.45, 41.47★.

Существование инвариантного подпространства размерности ≤ 2 для линейного оператора в конечномерном вещественном векторном пространстве.

Подстановка линейного оператора или матрицы в многочлен. Минимальный многочлен. Теорема Гамильтона–Кэли. Аналитические функции от линейных операторов и матриц над полем комплексных чисел.

Видеозапись лекции

Извлечение корней из невырожденных комплексных матриц. Вычисление значений многочленов и аналитических функций от линейных операторов и матриц путём сведения к многочленам степени < m, где m — степень минимального многочлена.

• 41.21, 41.22, 41.27, 41.30, 41.33, 42.19бгд, 42.20.

Экспонента линейного оператора/матрицы, её свойства, применение к решению систем однородных линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами.

Билинейные функции на векторных пространствах: определение, примеры (скалярное произведение геометрических векторов, определитель матрицы 2×2 как билинейная функция столбцов, след произведения матриц, интеграл произведения функций). Запись билинейных функций в координатах (билинейные формы), матрица билинейной функции, её преобразование при замене базиса. Ранг билинейной функции, невырожденные билинейные функции. Линейное отображение в сопряжённое пространство, задаваемое билинейной функцией, его матрица и критерий биективности. Сопряжённая билинейная функция и сопряжённое отображение. Симметрические и кососимметрические билинейные функции, примеры.

Видеозапись лекции

Примеры вычисления многочлена и экспоненты от матрицы. Билинейные функции, их матрицы. Классификация билинейных функций ранга 1.

• 37.1деиоу+37.2, 37.6б, 37.28, 37.30а★, 37.32аб.

Ортогональное дополнение к подпространству относительно симметрической или кососимметрической билинейной функции, его свойства, связь с аннулятором.

Квадратичные функции на векторном пространстве, ассоциированные с симметрическими билинейными функциями, их запись в координатах (квадратичные формы). Восстановление симметрической билинейной функции по ассоциированной квадратичной функции (формула поляризации). Канонический вид симметрических билинейных и квадратичных функций, алгоритм Лагранжа приведения к каноническому виду. Угловые миноры матрицы симметрической билинейной (или квадратичной) функции, метод Якоби приведения к каноническому виду.

Видеозапись лекции

Симметрические билинейные и квадратичные функции, поляризация. Приведение симметрической билинейной функции к каноническому виду алгоритмом Лагранжа и методом Якоби. Нахождение ортогонального дополнения к подпространству относительно симметрической билинейной функции.

• 38.5, 38.6б, 38.8, 38.9, 38.16б, 38.18бгзк, 38.29, 38.33.

Нормальный вид симметрических билинейных и квадратичных функций над полями C и R. Сигнатура и индексы инерции симметрической билинейной или квадратичной функции над R, закон инерции. Положительно определённые симметрические билинейные и квадратичные функции, критерий Сильвестра.

Евклидовы векторные пространства: определение, примеры (геометрические векторы, R^n со стандартным скалярным умножением, конечномерные подпространства в пространстве непрерывных функций на отрезке). Изоморфизм евклидовых пространств. Все евклидовы пространства одной размерности изоморфны друг другу.

Длина вектора в евклидовом пространстве, её простейшие свойства. Неравенство Коши–Буняковского. Неравенство треугольника.

Видеозапись лекции

Эквивалентность квадратичных форм над C и над R. При каких значениях параметра квадратичная функция положительно или отрицательно определена. Нормальный вид квадратичных функций над Z_p.

• 38.11ав, 38.14б, 38.17б, 38.19б, 38.21, 38.24, 38.30.

Угол между векторами в евклидовом пространстве, ортогональность векторов. Обобщённая теорема Пифагора. Ортогональные и ортонормированные базисы, ортогональные системы координат. Ортогональные матрицы, их характеризация как матриц перехода от одного ортонормированного базиса к другому.

Ортогональное дополнение к подпространству в евклидовом пространстве, его свойства. Ортогональная проекция и ортогональная составляющая вектора относительно подпространства. Матрица и определитель Грама, их свойства. Процесс ортогонализации Грама–Шмидта. Угол между вектором и подпространством достигается на ортогональной проекции вектора.

Видеозапись лекции

Нахождение ортогональной проекции и ортогональной составляющей вектора, угла между вектором и подпространством. Ортогонализация системы векторов. Свойства определителя Грама.

• 43.7бг, 43.11, 43.12, 43.15в, 43.19бв, 43.21б, 43.27, 43.38б, 43.41.

Канонический изоморфизм евклидова пространства V с V*. Взаимно однозначное соответствие между линейными операторами и билинейными функциями на евклидовом пространстве. Сопряжённый оператор, его матрица в ортонормированном базисе. Ортогональное дополнение к инвариантному подпространству инвариантно относительно сопряжённого оператора.

Ортогональные операторы, эквивалентные условия ортогональности, примеры. Определитель ортогонального оператора. Ортогональные группы: полная и специальная. Канонический вид матрицы ортогонального оператора.

Видеозапись лекции

Симметрические (самосопряжённые) и кососимметрические операторы. Наличие собственного вектора у симметрического оператора. Канонический вид матрицы симметрического и кососимметрического оператора. Приведение симметрических билинейных и квадратичных функций к главным осям.

Неотрицательные и положительно определённые симметрические операторы, пример: A*·A, где A — произвольный оператор. Критерий неотрицательности и положительной определённости симметрического оператора в терминах собственных значений. Извлечение квадратного корня из неотрицательного и положительно определённого оператора.

Полярное разложение невырожденного линейного оператора в евклидовом пространстве.

Видеозапись лекции

1. Нахождение базиса и системы уравнений для суммы двух подпространств (1 вариант), базиса и размерности пересечения двух подпространств (2 вариант).
2. Нахождение собственных векторов, жордановой нормальной формы и жорданова базиса для линейного оператора.
3. Вычисление экспоненты матрицы (1 вариант) и многочлена от матрицы (2 вариант).
4. Приведение симметрической билинейной формы (1 вариант) и квадратичной формы (2 вариант) к каноническому виду, выражение новых координат через старые.
5. Нахождение значений параметра, при которых квадратичная форма положительно определена (1 вариант); выяснение эквивалентности квадратичных форм над C и над R (2 вариант).

Псевдоевклидовы векторные пространства, ортонормированные базисы в них. Изотропные векторы и подпространства. Размерность максимальных изотропных подпространств. Изотропные подпространства одной размерности в псевдоевклидовом пространстве расположены одинаково. Псевдоортогональная группа. Пространство Минковского и геометрия Лобачевского.

Канонический вид кососимметрической билинейной функции, чётность её ранга.

Видеозапись лекции

Углы между векторами, количество векторов с попарными углами π/3. Ортогональные операторы, их собственные значения, ортогональность собственных подпространств. Приведение ортогонального оператора к каноническому виду.

• 43.40, 46.4, 46.6агж, 46.12, 46.14;
• найти канонический вид и соответствующий ортонормированный базис для ортогонального оператора, матрица которого в исходном ортонормированном базисе имеет вид:
• 

Симплектические векторные пространства, их размерность, симплектические базисы. Все симплектические пространства одной размерности изоморфны друг другу. Стандартный пример симплектического пространства: V = U⊕U*. Изотропные и лагранжевы подпространства в симплектическом пространстве. Симплектическая группа.

Комплексно сопряжённое векторное пространство. Полулинейные функции на комплексном векторном пространстве.

Видеозапись лекции

Сопряжённый оператор. Симметрические операторы, ортогональность собственных подпространств. Приведение симметрического оператора к каноническому виду. Приведение квадратичной функции к главным осям.

• 44.2, 44.5, 44.7, 45.4гж, 45.9, 45.18, 45.19деи.

Полуторалинейные функции на комплексном векторном пространстве, их запись в координатах. Матрица полуторалинейной функции, её преобразование при замене базиса. Эрмитово сопряжённые полуторалинейные функции и эрмитово сопряжённые матрицы. Эрмитовы и косоэрмитовы полуторалинейные функции, их матрицы. Эрмитовы квадратичные функции, формула поляризации. Положительно и отрицательно определённые эрмитовы функции. Нормальный вид эрмитовой полуторалинейной или квадратичной функции, закон инерции.

Эрмитовы векторные пространства, ортонормированные базисы в них, унитарные матрицы. Длина и ортогональность векторов в эрмитовом пространстве. Канонический изоморфизм эрмитова пространства V с пространством полулинейных функций на V.

Взаимно однозначное соответствие между линейными операторами и полуторалинейными функциями на эрмитовом пространстве. Эрмитово сопряжённый оператор, его матрица в ортонормированном базисе. Унитарные, эрмитовы и косоэрмитовы операторы, их матрицы в ортонормированном базисе. Нормальные операторы, их канонический вид.

Видеозапись лекции (без 5 минут в начале)

Положительно определённые симметрические операторы, извлечение квадратного корня. Полярное разложение линейного оператора.

• 45.12, 45.14, 45.15, 46.16абв (найти полярное разложение в обоих порядках);
• доказать, что всякая невырожденная вещественная матрица A может быть представлена в виде произведения A = U·D·V, где U и V — ортогональные матрицы, а D — диагональная матрица.

Унитарная группа. Положительно определённые эрмитовы операторы, извлечение квадратного корня. Полярное разложение невырожденного линейного оператора в эрмитовом пространстве, случай нормального оператора. Комплексификация евклидова пространства — эрмитово пространство. Комплексификация ортогонального, симметрического, кососимметрического оператора — унитарный, эрмитов, косоэрмитов оператор (соответственно).

Аффинные пространства: определение, примеры. Векторизация аффинного пространства, его размерность. Реперы и системы координат в аффинном пространстве, преобразование координат при замене репера. Плоскости в аффинном пространстве, способы их задания: с помощью опорной точки и направляющего подпространства, как аффинной оболочки множества точек, с помощью системы линейных уравнений.

Видеозапись лекции

Критические точки квадратичной функции на единичной сфере в евклидовом пространстве и собственные векторы симметрического оператора. Задание плоскостей в аффинном пространстве разными способами. Барицентрические линейные комбинации точек и барицентрические координаты в аффинном пространстве.

• 49.2, 49.5, 49.6б, 49.10б, 49.23;
• доказать, что собственные значения λ_1 ≥ … ≥ λ_n симметрического оператора A могут быть найдены по формулам λ_{k+1} = min_U max_x (x|Ax) и λ_{n-k} = max_U min_x (x|Ax), где U пробегает все подпространства коразмерности k, а x пробегает все точки единичной сферы в U;
• доказать, что множество из m точек аффинного пространства аффинно независимо тогда и только тогда, когда матрица, составленная из их барицентрических координат (записанных по строкам), имеет ранг m;
• с помощью барицентрических координат доказать теорему Менелая о точках, лежащих на сторонах треугольника (или их продолжениях).

Взаимное расположение плоскостей в аффинном пространстве, степень параллельности непересекающихся плоскостей, параллельные и скрещивающиеся плоскости.

Евклидовы аффинные пространства, ортогональные системы координат. Расстояние между точками в евклидовом пространстве, его свойства. Расстояние между плоскостями, формула для расстояния от точки до плоскости в терминах определителей Грама.

Видеозапись лекции

Взаимное расположение плоскостей в аффинном пространстве. Проведение через точку прямой, пересекающей две плоскости.

• 49.14, 49.16бв, 49.18, 49.20абв.

Объём многомерного параллелепипеда в евклидовом аффинном пространстве: индуктивное определение, выражение через определитель Грама и через определитель матрицы координат порождающих векторов в ортонормированном базисе.

Аффинные (аффинно-линейные) отображения аффинных пространств, их дифференциалы. Запись аффинного отображения в векторной форме и в координатах. Композиция аффинных отображений и её дифференциал. Изоморфизмы аффинных пространств, изоморфность аффинных пространств одной размерности. Существование и единственность аффинного отображения с заданным дифференциалом, переводящего заданную точку в заданный образ, и заданный максимальный набор аффинно независимых точек в другой заданный набор точек.

Группа Aff(S) аффинных преобразований аффинного пространства (S,V), подгруппы паралллельных переносов Tran(S) ≅ V и преобразований, сохраняющих начало отсчёта o ∈ S (изоморфна GL(V)). Разложение аффинного преобразования в композицию параллельного переноса и преобразования, сохраняющего начало отсчёта.

Видеозапись лекции

Матрица расстояний между точками евклидова пространства. Вычисление расстояния между плокостями.

• 51.2бг, 51.6а, 51.7в, 51.8, 51.14б, 51.15.

Движения (изометрии) евклидовых аффинных пространств. Группа Isom(S) движений евклидова аффинного пространства (S,V), её подгруппа движений, сохраняющих начало отсчёта o ∈ S (изоморфна O(V)). Разложение движения в композицию параллельного переноса и движения, сохраняющего начало отсчёта. Ось движения. Геометрическая классификация движений 2-мерного и 3-мерного евклидова пространства.

Квадратичные функции на аффинном пространстве, их запись в координатах. Расширенная матрица квадратичной функции, её преобразование при замене координат.

Видеозапись лекции

Аффинные отображения, их линейность относительно барицентрических комбинаций точек. Неподвижные точки аффинных преобразований и движений. Геометрическое описание движений 2-мерного и 3-мерного евклидова пространства.

• 49.27б, 49.28, 49.33а, 51.19б, 51.20, 51.21, 51.23бд, 51.24вг.

Центр квадратичной функции. Приведение квадратичной функции на аффинном пространстве к каноническому виду, к нормальному виду и к главным осям. Квадратичные гиперповерхности (квадрики) в аффинном пространстве. Единственность (с точностью до пропорциональности) уравнения, задающего квадрику (формулировка теоремы). Центр симметрии квадрики. Канонический вид уравнения, задающего квадрику; типы квадрик.

Видеозапись лекции

Приведение квадратичной функции к каноническому виду и к главным осям. Аффинная и метрическая классификация вещественных квадрик.

• 52.3, 52.6вг, 52.16, 52.19а, 52.20б, 52.22суф.

Доказательство теоремы о единственности уравнения, задающего квадрику.

Тензоры: определение, примеры тензоров малых валентностей (скаляры, ковекторы, векторы, билинейные функции, сопоставление линейному оператору тензора типа (1,1)), определитель как тензор типа (n,0). Операции над тензорами: сложение, умножение на скаляры, тензорное умножение, их свойства.

Тензорный базис пространства тензоров типа (p,q), его размерность, компоненты тензора. Правило Эйнштейна.

Видеозапись лекции

Вычисление значений и компонент тензоров в разных базисах. Разложимость тензоров в тензорное произведение.

• 47.1бвге, 47.2, 47.3б, 47.4, 47.7;
• тензор det не разложим в тензорное произведение тензоров меньшей валентности.

Операции над тензорами в координатах. Преобразование компонент тензора при замене базиса в основном пространстве. Изоморфизм пространств линейных операторов и тензоров типа (1,1) над основным пространством.

Свёртка тензоров: определение и примеры (спаривание векторов и ковекторов, значение тензора на наборе векторов и ковекторов, след линейного оператора, применение линейного оператора к вектору и произведение линейных операторов). Подъём и опускание индексов у тензоров.

Видеозапись лекции

Тензоры типа (1,1) и линейные операторы. Свёртка тензоров. Тензорное произведение линейных операторов, его след.

• 47.9б, 47.10, 47.12, 47.13бв, 47.14б, 47.15б, 47.16абг, 47.18бв.

Ковариантные и контравариантные тензоры. Симметрические и кососимметрические тензоры. Операции симметризации и альтернирования тензоров, их свойства.

Внешнее умножение кососимметрических тензоров, его свойства: антикоммутативность, ассоциативность, внешнее произведение векторов и ковекторов, его связь с определителями. Базис и размерность пространства кососимметрических тензоров данной степени. Критерии линейной независимости набора векторов и принадлежности вектора подпространству в терминах внешнего умножения. Соответствие между подпространствами и вполне разложимыми поливекторами.

Видеозапись лекции

Матрица двойственного метрического тензора. Подъём и опускание индексов у тензора. Приведение кососимметрической билинейной функции к каноническому виду с использованием внешнего умножения.

• 37.33авг, 48.13, 48.14, 48.15, 48.16.

1. Ортогонализация системы векторов (1 вариант); вычисление объёма параллелепипеда (2 вариант).
2. Нахождение угла между вектором и подпространством (1 вариант); вычисление расстояния от точки до плоскости (2 вариант).
3. Приведение симметрической билинейной формы (1 вариант) и квадратичной формы (2 вариант) к главным осям.
4. Определение типа движения плоскости (1 вариант) и пространства (2 вариант) и его полное геометрическое описание.
5. Полярное разложение невырожденного линейного оператора.