Тема 3
Присоединённое представление полной линейной группы: примыкание орбит
Здесь основное поле $\mathbb{K}=\mathbb{R}$ или $\mathbb{C}$. Сохраняются обозначения предыдущего семинара.
Каждое множество уровня инвариантов присоединённого представления $Z_c$ распадается на конечное число орбит группы $GL(V)$ (эти орбиты параметризуются всевозвожными жордановыми нормальными формами операторов с данным характеристическим многочленом). Обозначим через $\mathcal{O}_{\mathcal{A}}$ орбиту оператора $\mathcal{A}$.
Определение 1. Орбита $\mathcal{O}_{\mathcal{B}}$ примыкает к орбите $\mathcal{O}_{\mathcal{A}}$, если содержится в её замыкании: $\mathcal{O}_{\mathcal{B}}\subset\overline{\mathcal{O}_{\mathcal{A}}}$.
Поскольку каждое множество уровня $Z_c$ замкнуто, то примыкать друг к другу могут только орбиты из одного и того же множества уровня.
Вопрос 1. Как устроено отношение примыкания на множестве орбит в $Z_c$?
Если $\mathcal{O}_{\mathcal{B}}\subset\overline{\mathcal{O}_{\mathcal{A}}}$, то можно без ограничения общности считать, что полупростые части операторов $\mathcal{A}$ и $\mathcal{B}$ одинаковы: $\mathcal{A}_s=\mathcal{B}_s=\mathcal{S}$.
Рассмотрим централизатор оператора $\mathcal{S}$ — пространство $Z(\mathcal{S})$ операторов, коммутирующих с $\mathcal{S}$. Если $\mathbb{K}=\mathbb{C}$, то имеет место разложение $V=V_{\lambda_1}\oplus\dots\oplus V_{\lambda_m}$ в прямую сумму собственных подпространств оператора $\mathcal{S}$, и централизатор состоит из блочно-диагональных операторов:
Теорема 1. $\mathcal{O}_{\mathcal{B}}\subset\overline{\mathcal{O}_{\mathcal{A}}}\iff\mathcal{O}'_{\mathcal{B}_n}\subset\overline{\mathcal{O}'_{\mathcal{A}_n}}$.
В теореме нетривиальна лишь импликация "$\implies$". Для её доказательства можно рассмотреть последовательность операторов $\mathcal{A}(k)\in\mathcal{O}_{\mathcal{A}}$, сходящуюся к $\mathcal{B}$. При этом $\mathcal{A}(k)_s\in\mathcal{O}_{\mathcal{S}}$, т.е. $\mathcal{A}(k)_s=\mathcal{C}(k)\,\mathcal{S}\,\mathcal{C}(k)^{-1}$. Поскольку $\mathcal{A}(k)_s$ и $\mathcal{B}_s=\mathcal{S}$ выражаются (одинаковыми) многочленами от $\mathcal{A}(k)$ и $\mathcal{B}$ (Задача 1.4), $\mathcal{A}(k)_s\to\mathcal{B}_s=\mathcal{S}$ и $\mathcal{A}(k)_n\to\mathcal{B}_n$ при $k\to\infty$. Можно считать, что $\mathcal{C}(k)\to\mathcal{E}$ при $k\to\infty$ (Задача 3.2). Заменив $\mathcal{A}(k)$ на $\mathcal{C}(k)^{-1}\,\mathcal{A}(k)\,\mathcal{C}(k)$, можно считать, что $\mathcal{A}(k)_s=\mathcal{S}$. Но тогда $\mathcal{A}(k)=\mathcal{H}(k)\,\mathcal{A}\,\mathcal{H}(k)^{-1}$, где $\mathcal{H}(k)\in Z(\mathcal{S})$, и $\mathcal{A}(k)_n=\mathcal{H}(k)\,\mathcal{A}_n\,\mathcal{H}(k)^{-1}\to\mathcal{B}_n$, т.е. $\overline{\mathcal{O}'_{\mathcal{A}_n}}\supset\mathcal{O}'_{\mathcal{B}_n}$.
Теорема 1 сводит вопрос к орбитам нильпотентных операторов.
Вопрос 2. Как устроено отношение примыкания на множестве нильпотентных орбит?
Орбиты нильпотентных операторов в $n$-мерном пространстве параметризуются разбиениями числа $n$, т.е. такими последовательностями натуральных чисел $p=(p_1,\dots,p_m)$, что $p_1\ge\dots\ge p_m$ и $p_1+\dots+p_m=n$ (обозначение: $p\vdash n$). Числа $p_j$ — это размеры жордановых клеток матрицы нильпотентного оператора. Удобно изображать разбиения диаграммами Юнга:
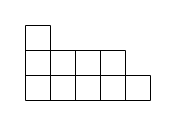
Определение 2. Частичный порядок на разбиениях (или диаграммах Юнга): $p\succeq q$, если $p_1+\dots+p_k\ge q_1+\dots+q_k$ ($\forall k$).
Теорема 2. $\overline{\mathcal{O}_p}\supset\mathcal{O}_q\iff p\succeq q$.
Импликация "$\implies$" основана на том, что для $\mathcal{A}\in\mathcal{O}_p$, $\mathcal{B}\in\mathcal{O}_q$ выполнены неравенства $\dim\operatorname{Ker}(\mathcal{A}^k)\le\dim\operatorname{Ker}(\mathcal{B}^k)$ ($\forall k$), и на задаче 3.3. Доказательство импликации "$\impliedby$" содержится в задачах 3.4—3.5.
Задача 3.1. Пусть последовательность операторов $\mathcal{A}(k)$ (не обязательно лежащих в одном множестве уровня), сходится к оператору $\mathcal{B}$. Верно ли, что $\mathcal{A}(k)_s\to\mathcal{B}_s$, $\mathcal{A}(k)_n\to\mathcal{B}_n$?
Задача 3.2. Если последовательность сопряжённых друг другу полупростых операторов $\mathcal{S}(k)$ сходится к оператору $\mathcal{S}$, то $\mathcal{S}(k)=\mathcal{C}(k)\,\mathcal{S}\,\mathcal{C}(k)^{-1}$, причём $\mathcal{C}(k)\to\mathcal{E}$.
Задача 3.3. $p\succeq q\iff p^{\top}\preceq q^{\top}$, где $p^{\top}$ обозначает разбиение, отвечающее транспонированной диаграмме Юнга.
Задача 3.4. $p\succeq q$ тогда и только тогда, когда $q$ получается из $p$ цепочкой осыпаний, где под осыпанием диаграммы Юнга $p$ понимается переход к диаграмме $p'$, которая получается из $p$ перемещением верхней клетки какого-либо столбца в следующий столбец наверх (осыпание 1-го типа) или правой клетки какой-либо строки в конец предыдущей строки (осыпание 2-го типа).
Задача 3.5. Если $p'$ получается из $p$ осыпанием, то $\mathcal{O}_{p'}\subset\overline{\mathcal{O}_p}$ (достаточно рассмотреть осыпание 1-го типа, в котором обе диаграммы состоят не более чем из двух столбцов).
Задача 3.6. Если $\mathcal{A}\in\mathcal{O}_p$, то $\dim Z(\mathcal{A})=\sum_j(p^{\top}_j)^2$.