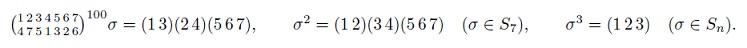Преподаватель: Д.А.Тимашёв

Занятия проходят по понедельникам на каждой нечётной неделе на 1-й паре (9:00-10:35) в ауд. 406 и по средам на 1-й паре (9:00-10:35) в ауд. 16-13.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.

<fc #FF0000>Коллоквиум</fc> пройдёт на семинаре в среду 24 октября.

<fc #FF0000>Контрольная работа</fc> пройдёт на семинаре в среду 7 ноября.

Системы линейных уравнений (СЛУ), их решение методом Гаусса. Связь решений совместной СЛУ и ассоциированной однородной системы линейных уравнений (ОСЛУ). Критерии определённости совместной СЛУ и квадратной СЛУ: ассоциированная ОСЛУ должна быть определена. Задача интерполяции, теорема о полиномиальной интерполяции.

• 8.1вг, 8.2вг, 8.8;
• ★ найти явную формулу для интерполяционного многочлена.

Метод Крамера решения квадратных СЛУ малых размеров (2×2 и 3×3). Определители 2-го и 3-го порядка.

• 8.6вд, 8.2е, 9.1гд, 9.2ж, 16.1б.

Линейная зависимость, базис системы векторов, координаты вектора в базисе. Стандартный базис в R^n. Когда система векторов обладает единственным базисом? Ранг системы векторов и размерность пространства. Алгоритм нахождения базиса конечной системы векторов в R^n.

• 6.4, 6.13, 6.14, 6.12вги, 7.19★.

Вычисление ранга матрицы. Фундаментальная система решений ОСЛУ.

• 7.1дл, 7.2аз, 7.5, 7.7, 7.10, 8.4вг, 8.25★.

Арифметические операции над матрицами (сложение матриц, умножение матриц на числа, умножение матриц), их свойства, некоммутативность умножения матриц, делители нуля и нильпотентные матрицы, нильпотентность нильтреугольных матриц.

• 17.1бв, 17.4ав, 17.25, 19.26, 19.15, 19.18, 17.26★.

Умножение на диагональные матрицы и матричные единицы. Квадратные матрицы, коммутирующие со всеми матрицами того же размера, скалярны. Единичная матрица. Обратная матрица. Если матрица A нильпотентна, то матрицы E+A и E-A обратимы. Нахождение обратной матрицы сводится к решению матричных уравнений вида AX=B, алгоритм их решения.

• 17.17, 18.3взи, 18.17★, 19.14, 19.21.

Вычисление обратной матрицы с помощью элементарных преобразований. Матрица, обратная к транспонированной. Элементарные матрицы, умножение на них слева и справа.

Умножение подстановок. Разложение подстановки на независимые циклы, применение к возведению подстановок в степень. Решение уравнений в подстановках.

• 18.9кл, 19.3аг, 3.1вг, 3.2аге, 3.13;
• как изменится A^{-1}, если матрицу A подвергнуть одному из следующих преобразований:
  • записать её строки в обратном порядке;
  • транспонировать относительно побочной диагонали;
  • повернуть на 90º против часовой стрелки?
• решить уравнения в подстановках:
  • 
• (задача о квартирном обмене) Несколько семей хотят обменяться квартирами. За один день каждая семья может принять участие не более чем в одном обмене квартирами с какой-нибудь другой семьей. Доказать, что любой сложный обмен можно осуществить не более чем за два дня.

Чётность и знак перестановок и подстановок. Знак цикла. Задача про «пятнашки»: можно ли, последовательно передвигая фишки на соседнее свободное место, поменять местами фишки 14 и 15, оставив остальные фишки на месте? Можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы угловые кубики одной из граней переставились по кругу, а остальные кубики остались на своих местах (возможно, повернувшись)?

Определители квадратных матриц, их вычисление по развёрнутой формуле.

• 3.6бвж, 3.11, 3.22, 10.4б, 16.2, 11.1, 11.4;
• можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы один из боковых кубиков в нём перевернулся, а остальные остались на своих местах, не изменив положения?

Поведение определителя при различных преобразованиях матрицы. Вычисление определителей приведением к треугольному виду и приведением к определителю Вандермонда.

• 13.1бвж, 13.2ежз, 14.1зкм★н.

Определитель произведения матриц. Разложение определителя по строке и по столбцу.

• 12.2, 12.3дези, 15.2бв, 16.19.

Вычисление определителей с помощью рекуррентных соотношений. Трёхдиагональные определители и линейные однородные рекуррентные уравнения 2-го порядка.

• 14.1гдео, 12.4, 4.5, 16.3, 11.10е;
• вычислить определитель:
•