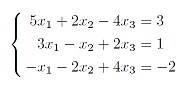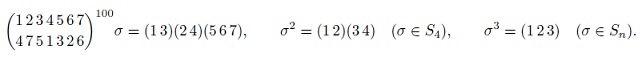Кафедра высшей алгебры

Преподаватель: Д.А.Тимашёв

Занятия проходят дистанционно в Zoom по четвергам на 2-й паре (11:00-12:35) и по субботам на каждой чётной неделе на 1-й паре (9:00-10:35).

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Факториал, 2001. Дополнительные задачи помечены знаком ★.

Системы линейных уравнений (СЛУ). Метод Крамера решения квадратных СЛУ малых размеров (2×2 и 3×3). Определители 2-го и 3-го порядка.

• 8.6вд, 8.2е, 9.1гд, 9.2ж, 16.1а;
• решить методом Крамера систему линейных уравнений:
• 

Решение СЛУ методом Гаусса. Связь решений совместной СЛУ и ассоциированной однородной системы линейных уравнений (ОСЛУ). Критерии определённости совместной СЛУ и квадратной СЛУ: ассоциированная ОСЛУ должна быть определена. Задача интерполяции, теорема о полиномиальной интерполяции.

• 8.1вг, 8.2вг, 8.8;
• ★ найти явную формулу для интерполяционного многочлена.

Линейная зависимость, базис системы векторов (три эквивалентных определения), координаты вектора в базисе. Стандартный базис в R^n. Когда система векторов обладает единственным базисом? Алгоритм нахождения базиса конечной системы векторов в R^n.

• 6.4, 6.13, 6.14, 6.12авги, 7.19★.

Ранг матрицы, его свойства. Вычисление ранга матрицы.

• 7.1дл, 7.2аз, 7.6, 7.7, 7.10.

Фундаментальная система решений ОСЛУ. Арифметические операции над матрицами (сложение матриц, умножение матриц на числа, умножение матриц), их свойства, некоммутативность умножения матриц, Умножение на диагональные матрицы, нулевая и единичная матрицы.

• 8.4вг, 8.25★, 17.1бв, 17.4ав, 17.25, 19.26.

Делители нуля и нильпотентные матрицы, нильпотентность нильтреугольных матриц. Матричные единицы. Квадратные матрицы, коммутирующие со всеми матрицами того же размера, скалярны.

• 17.17, 17.18, 17.26, 19.14, 19.15.

Обратная матрица. Если матрица A нильпотентна, то матрицы E+A и E-A обратимы. Решение матричных уравнений вида AX=B. Нахождение обратной матрицы. Элементарные матрицы, умножение на них слева и справа.

• 18.3взи, 18.9кл, 18.17★, 19.3ав, 19.21.

Умножение подстановок. Разложение подстановки на независимые циклы, применение к возведению подстановок в степень. Решение уравнений в подстановках. Чётность и знак перестановок и подстановок.

• 3.1вг, 3.2аге, 3.3ав, 3.4аб, 3.6бвж, 3.13;
• решить уравнения в подстановках:
• 
• (задача о квартирном обмене) Несколько семей хотят обменяться квартирами. За один день каждая семья может принять участие не более чем в одном обмене квартирами с какой-нибудь другой семьей. Доказать, что любой сложный обмен можно осуществить не более чем за два дня.

Знак циклической подстановки. Задача про «пятнашки»: можно ли, последовательно передвигая фишки на соседнее свободное место, поменять местами фишки 14 и 15, оставив остальные фишки на месте? Можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы угловые кубики одной из граней переставились по кругу, а остальные кубики остались на своих местах (возможно, повернувшись)?

Определители квадратных матриц, их вычисление по развёрнутой формуле. Поведение определителя при различных преобразованиях матрицы.

• 3.22, 10.4б, 11.1гд, 11.4, 16.2;
• можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы один из боковых кубиков в нём перевернулся, а остальные остались на своих местах, не изменив положения?

Вычисление определителей приведением к треугольному виду и приведением к определителю Вандермонда. Разложение определителя по строке и столбцу.

• 13.1бвж, 13.2ежз, 14.1зкм★н, 12.2.

Вычисление определителей разложением по строке и столбцу. Трёхдиагональные определители и линейные однородные рекуррентные уравнения 2-го порядка.

• 12.3ези, 14.1где, 12.4, 4.5;
• вычислить определитель:
• 

Вычисление трёхдиагонального определителя в случае кратного корня характеристического уравнения. Определитель произведения матриц. Ранг произведения матриц, случай невырожденности одного из сомножителей. Ранг присоединённой матрицы.

• 7.11, 15.2бвг, 16.4, 16.19.

Кольца и поля вычетов. Решение СЛУ и квадратных уравнений над полями вычетов. Использование колец вычетов для решения диофантовых уравнений (примеры: 23x-17y=5, 3x²+2=y², 7x²+2=y³). Малая теорема Ферма. Обратимые элементы кольца вычетов, функция Эйлера, теорема Эйлера. Задача: последовательность k_1=2, k_{n+1}=2^{k_n} стабилизируется по модулю 7. Квадратичные вычеты, символ Лежандра.

• 66.20, 8.10б, 66.24вг, 66.23ав, 66.32;
• решить диофантовы уравнения: 41x-11y=19, 35x+21y=14, 15x²-7y²=9;
• доказать, что для любых a∈Z и m∈N последовательность k_1=a, k_{n+1}=a^{k_n} стабилизируется по модулю m;
• ★ доказать, что символ Лежандра элемента a∈Z_p равен знаку подстановки на множестве Z_p\{0}, задаваемой умножением на a.

1. Решение СЛУ в зависимости от параметра.
2. Нахождение ФСР и размерности пространства решений ОСЛУ (1 вариант); нахождение базиса системы векторов и выражение через него остальных векторов системы (2 вариант).
3. Нахождение обратной матрицы (1 вариант); решение матричного уравнения (2 вариант).
4. Вычисление определителя размера 4×4.
5. Вычисление определителя размера n×n.
6. Решение уравнения в подстановках (1 вариант); вычисление трёхдиагонального определителя (2 вариант).

Вычисления над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, решение алгебраических задач геометрическими методами (пример: уравнение |(z-1+i)/(z+1-i)|=1) и геометрических задач методами алгебры комплексных чисел (пример: доказательство теоремы о том, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон).

Тригонометрическая форма записи комплексных чисел, вычисления над комплексными числами в тригонометрической форме. Выражение тригонометрических функций кратных углов через функции исходного угла и степеней тригонометрических функций через функции кратных углов в первой степени с помощью комплексных чисел.

• 20.1еж, 21.2бж, 21.9аг, 21.10, 21.12, 21.13в;
• доказать с помощью комплексных чисел теорему Птолемея: произведение диагоналей четырёхугольника, вписанного в окружность, равно сумме произведений его противоположных сторон.

Извлечение корней из комплексных чисел. Группа U_n комплексных корней степени n из 1, сумма и произведение всех корней степени n из 1. Вычисление сумм с помощью комплексных чисел.

• 22.7еипр, 22.8а, 22.9б, 22.17аб, 22.22★, 23.1вг, 23.2бв.

Многочлены от одной переменной над полем K: деление с остатком, теорема Безу, схема Горнера. Разложение многочлена по степеням линейного двучлена, значения высших производных и кратность корня многочлена.

• 25.1б, 26.1бв, 26.2бв, 26.3бв, 26.4, 26.6, 26.7бв, 26.11★.

Наибольший общий делитель (НОД) многочленов и алгоритм Евклида. Линейное выражение НОД через исходные многочлены: (f,g)=uf+vg, его единственность при ограничениях на степени u и v, и его нахождение методом неопределённых коэффициентов. Избавление от кратных множителей в разложении многочлена на неприводимые множители.

• 25.2вг, 25.3б, 25.5б, 25.7бв, 25.8б;
• найти НОД многочленов x^n-1 и x^m-1.

Разложение многочленов на неприводимые множители над полями C и R. Неприводимых многочленов над любым полем бесконечно много. Существование неприводимых многочленов сколь угодно большой степени над конечным полем. «Решето Эратосфена» для нахождения всех неприводимых многочленов степени ≤n над конечным полем. Нахождение всех неприводимых многочленов степени ≤3 над полем Z_2.

• 27.1ад, 27.2бге, 27.6, 27.7, 27.12, 27.14★, 28.23;
• найти все неприводимые многочлены степеней 4 и 5 над полем Z_2;
• найти все неприводимые многочлены степени ≤3 со старшим коэффициентом 1 над полем Z_3;
• найти количество неприводимых многочленов степени 4 со старшим коэффициентом 1 над полем Z_3.

Над полем Q существуют неприводимые многочлены любой степени. Рациональные корни многочлена с целыми или рациональными коэффициентами. Разложимость многочлена с целыми коэффициентами на множители меньшей степени в Q[x] равносильна разложимости на множители меньшей степени в Z[x]. Редукция многочленов с целыми коэффициентами по простому модулю, её свойства. Редукционный признак неприводимости. Разложение многочленов на неприводимые множители над Q с помощью редукций.

• 28.1в, 28.2бвж, 28.9вде;
• разложить на множители над Z:
  1. 3x^5-2x^4+5x^3-4x^2-5x-1,
  2. 2x^4-3x^3+5x^2+8x-5,
  3. 3x^4-x^3+5x^2+8x-7;
• ★ доказать, что многочлен x^4-10x^2+1 неприводим над Q, но его редукция по любому простому модулю p приводима над Z_p.

Признак Эйзенштейна, неприводимость многочлена деления круга на простое число частей.

Рациональные дроби: представление в виде суммы многочлена и правильной дроби, разложение правильной дроби в сумму простейших дробей методом неопределённых коэффициентов, случай полей C и R.

• 28.9аб, 29.1бе, 29.2аги, 29.3.

Симметрические многочлены: основная теорема, метод неопределённых коэффициентов для нахождения выражения произвольного симметрического многочлена через элементарные. Выражение степенных сумм s_1, s_2, s_3, s_4 через элементарные симметрические многочлены. Теорема Виета. Решение симметрических систем алгебраических уравнений.

• 31.2, 31.7, 31.9авер, 31.15, 31.21б, 31.25.

1. Возведение в степень (1 вариант) и извлечение корней (2 вариант) в поле C.
2. Нахождение НОД двух многочленов и его линейного выражения через эти многочлены.
3. Разложение многочлена на неприводимые множители над полем R (1 вариант); разложение многочлена по степеням линейного двучлена, определение кратности корня и вычисление значений высших производных (2 вариант).
4. Разложение многочлена на неприводимые множители над полем Q.
5. Разложение рациональной дроби в сумму многочлена и простейших дробей над полем C (1 вариант) и R (2 вариант).
6. Выражение симметрического многочлена через элементарные симметрические многочлены.