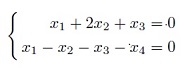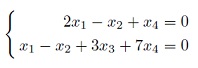Семинары, 108 группа
Преподаватель: Д.А.Тимашёв
Занятия проходят по средам и пятницам на 2-й паре (10:45-12:20) в ауд. 463.
Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.
7 февраля 2018
Векторные пространства: простейшие следствия из аксиом, примеры (в частности: множество 2^X всех подмножеств множества X как векторное пространство над Z_2, абелеву группу Z нельзя превратить в векторное пространство). Линейные комбинации векторов, линейная зависимость, примеры линейно независимых систем функций.
Домашнее задание:
- 34.3дж, 34.4аб, 34.5, 34.7бг;
- доказать, что множество R^+ положительных чисел с операциями u⊕v = u·v (u,v∈R^+) и λ⊗v = v^λ (λ∈R, v∈R^+) является векторным пространством над полем R.
9 февраля 2018
Базис, размерность, координаты. Матрица перехода к другому базису, её свойства, преобразование координат вектора при замене базиса. Расширения полей как векторные пространства, число элементов конечного поля. Подпространства, примеры.
Домашнее задание:
- 34.8д★з, 34.10ав, 34.11а, 34.12, 35.3вгдеж, 35.10.
14 февраля 2018
Способы задания подпространств (линейная оболочка и однородная система линейных уравнений). Базис, согласованный с подпространством. Пересечение и сумма двух подпространств (объединение — вообще говоря, не подпространство). Базис, согласованный с парой подпространств, формула Грассмана для размерности их суммы (пример: 7-мерное подпространство пространства матриц размера 4×4 содержит ненулевую симметрическую матрицу). Инварианты взаимного расположения пары подпространств, обсуждение инвариантов троек и четвёрок подпространств (в последнем случае дискретных инвариантов недостаточно, пример: двойное отношение четвёрки прямых на плоскости). Прямая сумма подпространств, проекции на прямые слагаемые (пример: разложение пространства квадратных матриц в прямую сумму подпространств симметрических и кососимметрических матриц).
Домашнее задание:
- 35.9, 35.18, 35.22, 35.24, 35.26, 35.27;
- если матрица A размера n×n имеет ранг ≤n/2, то матричное уравнение AX=0 имеет решением ненулевую треугольную матрицу X;
- ★ найти полную систему инвариантов взаимного расположения трёх подпространств в конечномерном векторном пространстве.
16 февраля 2018
Линейные функции на векторном пространстве V, их координатная запись. Ядро линейной функции. Сопряжённое пространство V*, сопряжённый базис. Канонический изоморфизм пространств V и (V*)* в конечномерном случае. Двойственность между векторами и линейными функциями (ковекторами).
Аннулятор подпространства, его размерность. Совпадение второго аннулятора подпространства с этим подпространством в конечномерном случае. Задание подпространства однородной системой линейных уравнений ⇔ нахождение базиса аннулятора подпространства.
Домашнее задание:
- 36.14, 36.18, 36.17, 35.16б, 36.15, 36.20, 35.25.
21 февраля 2018
Критерий базисности набора ковекторов, применение: интерполяционная формула Лагранжа. Нахождение суммы и пересечения подпространств.
Линейные отображения, их матрицы, запись линейного отображения в координатах. Преобразование матрицы линейного отображения при замене базисов.
Домашнее задание:
- 35.15в, 36.2, 36.3;
- доказать что линейные функции β_i(f) = f^(i)(x_0) (i=0,…,n) образуют базис сопряжённого пространства к пространству многочленов степени ≤n над полем характеристики 0, найти двойственный к нему базис и написать разложение произвольного многочлена степени ≤n по этому базису;
- задать системой однородных линейных уравнений сумму подпространств U+W в 4-мерном пространстве V при условии, что подпространства U и W заданы с помощью ОСЛУ:
28 февраля 2018
Ядро и образ линейного отображения. Канонический вид матрицы линейного отображения. Линейные операторы в векторном пространстве, их матрицы. Преобразование матрицы линейного оператора при замене базиса.
Домашнее задание:
- 36.8, 39.13, 39.15гли, 39.19.
2 марта 2018
Инвариантные подпространства линейного оператора. Собственные векторы и собственные значения. Характеристический многочлен, его коэффициенты. Собственные подпространства, их линейная независимость. Алгебраическая и геометрическая кратности собственного значения. Диагонализуемые операторы, эквивалентные условия диагонализуемости.
Домашнее задание:
- 40.5, 40.7, 40.9, 40.11★, 40.15ге, 40.16авг, 40.22, 40.24бвг, 40.33★.
7 марта 2018
Корневые векторы и корневые подпространства линейного оператора, их инвариантность, размерность и линейная независимость. Нильпотентные операторы: жорданов базис, диаграммы Юнга. Жорданова нормальная форма (ЖНФ) линейного оператора, формулы для количества жордановых клеток с заданным собственным значением (всех и данного размера).
Домашнее задание:
- 41.1агжим, 41.3, 41.5, 41.7, 41.10бвг.
14 марта 2018
Нахождение ЖНФ и жорданового базиса для линейного оператора. Применения ЖНФ: критерий нильпотентности линейного оператора в терминах собственных значений, нижняя оценка размерности централизатора линейного оператора.
Домашнее задание:
- 41.14★, 41.15, 41.18, 41.20, 41.22, 41.45, 15.3.
16 марта 2018
Многочлены от линейных операторов и матриц. Аннулирующие многочлены, теорема Гамильтона–Кэли. Минимальный многочлен, его свойства и вычисление. Вычисление многочлена от линейного оператора (матрицы) нахождением остатка при делении на минимальный многочлен. Аналитические функции от линейных операторов и матриц.
Домашнее задание:
21 марта 2018
Пример: вычисление экспоненты матрицы.
Билинейные функции, их запись в координатах (билинейные формы). Матрица билинейной функции, её преобразование при замене базиса. Ранг билинейной функции. Классификация билинейных функций ранга ≤1.
Домашнее задание:
- 37.1джмнпсту, 37.2, 37.6, 37.25, 37.28аб.
23 марта 2018
Дискриминант, невырожденные билинейные функции. Симметрические и кососимметрические билинейные функции, разложение пространства билинейных функций в прямую сумму подпространств симметрических и кососимметрических функций. Квадратичные функции, поляризация. Канонический вид симметрических билинейных и квадратичных функций, методы Лагранжа и Якоби приведения к каноническому виду.
Домашнее задание:
- 37.30а★, 38.3, 38.4, 38.8б, 38.9, 38.16б, 38.18бвгзк, 38.33.
28 марта 2018
Нормальный вид квадратичных функций над полями C и R, закон инерции. Неотрицательные и положительно определённые квадратичные фукнции, критерий Сильвестра. Геометрический смысл индексов инерции.
Домашнее задание:
- 38.11б, 38.14а, 38.17б, 38.19, 38.21, 38.22а, 38.30.
30 марта 2018
4 апреля 2018
Контрольная работа
- Нахождение базиса и системы линейных уравнений для суммы двух подпространств, заданных системами линейных уравнений (1 вариант); нахождение размерности и базиса пересечения двух подпространств, заданных своими базисами (2 вариант).
- Нахождение собственных векторов и жордановой нормальной формы линейного оператора.
- Вычисление экспоненты матрицы (1 вариант) и многочлена от матрицы (2 вариант).
- Приведение симметрической билинейной формы (1 вариант) и квадратичной формы (2 вариант) к каноническому виду.
- Выяснение положительной определённости квадратичной формы в зависимости от значений параметра (1 вариант); выяснение эквивалентности двух квадратичных форм над полями C и R (2 вариант).
6 апреля 2018
Евклидовы векторные пространства. Длина вектора, её свойства. Неравенство Коши–Буняковского. Ортогональность векторов, линейная независимость ортогональной системы ненулевых векторов. Обобщённая теорема Пифагора. Ортогональные и ортонормированные базисы, ортогональные системы координат. Ортогональное дополнение к подпространству, его свойства. Ортогональная проекция и ортогональная составляющая вектора относительно подпространства. Процесс ортогонализации Грама–Шмидта. Матрица и определитель Грама, их свойства.
Домашнее задание:
- 43.7г, 43.11, 43.12, 43.15в, 43.18а, 43.19бв, 43.27.
11 апреля 2018
Объём многомерного параллелепипеда в евклидовом пространстве. Вычисление объёма параллелепипеда, натянутого на одночлены 1, x, x², в пространстве многочленов со скалярным умножением (f|g)=∫fgdx (интеграл по [-1,1]). Расстояние между векторами в евклидовом пространстве, его свойства. Расстояние между вектором и подпространством.
Домашнее задание:
- 43.45а (при n=3, ★ при любом n), 43.36а (вычислить объём двумя способами), 43.37, 43.21б, 43.24.
13 апреля 2018
Угол между векторами, линейная независимость системы векторов с попарными углами π/3. Угол между вектором и подпространством.
Ортогональные операторы и их матрицы, примеры: поворот плоскости и пространства, отражение относительно подпространства. Свойства ортогональных операторов: сохранение длин, расстояний. Всякая линейная изометрия евклидова пространства — ортогональный оператор.
Домашнее задание:
- 43.38б, 43.40, 43.41, 46.4, 46.12, 46.14;
- ★ всякая изометрия евклидова пространства является композицией ортогонального оператора и сдвига.
18 апреля 2018
Свойства ортогональных операторов: сохранение углов, возможные собственные значения, ортогональность собственных подпространств, инвариантность ортогонального дополнения к инвариантному подпространству. Канонический вид матрицы ортогонального оператора, его нахождение. Комплексификация вещественных векторных пространств и линейных операторов, нахождение 2-мерного инвариантного подпространства для линейного оператора над R, не имеющего собственных векторов.
Домашнее задание:
20 апреля 2018
Соответствие между линейными операторами и билинейными функциями в евклидовом пространстве. Сопряжённый оператор, его матрица. Подпространство U инвариантно относительно оператора A ⇒ ортогональное дополнение к U инвариантно относительно сопряжённого оператора A*. Оператор A ортогонален ⇔ A* обратен к A.
Симметрические (самосопряжённые) и кососимметрические операторы. Наличие собственного вектора и ортогональность собственных подпространств симметрического оператора. Канонический вид матрицы симметрического оператора, его нахождение. Приведение симметрических билинейных и квадратичных функций к главным осям.
Домашнее задание:
- 44.1бвгде, 44.2, 44.5, 44.7, 45.4гж, 45.18, 45.19деи.
25 апреля 2018
Неотрицательные и положительно определённые симметрические операторы, пример: A*·A, где A — произвольный оператор в евклидовом пространстве. Критерий неотрицательности и положительной определённости симметрического оператора в терминах собственных значений. Извлечение квадратного корня из неотрицательного и положительно определённого оператора. Полярное разложение невырожденного линейного оператора в евклидовом пространстве.
Домашнее задание:
- 45.12, 45.14, 45.15, 45.16бв;
- всякая невырожденная вещественная матрица A представляется в виде A=U·D·V, где U и V — ортогональные матрицы, а D — диагональная матрица;
- ★ у любого линейного оператора A (возможно, вырожденного) существуют (не обязательно единственные) полярные разложения в виде A=U·R=S·V, где U,V — ортогональные, а R,S — неотрицательные симметрические операторы.
27 апреля 2018
Аффинные пространства. Векторизация. Координаты в аффинном пространстве, замена координат. Плоскости в аффинном пространстве, способы их задания (опорная точка + направляющее подпространство, параметрический способ, аффинная оболочка, система линейных уравнений). Взаимное расположение плоскостей в аффинном пространстве, размерность аффинной оболочки их объединения и их пересечения, степень параллельности.
Домашнее задание:
- 49.3, 49.10б, 49.12, 49.16ав, 49.20а.
4 мая 2018
Задача: провести через точку прямую, пересекающую две плоскости. Евклидовы аффинные пространства: расстояние между точками, задача: может ли данная матрица быть матрицей расстояний между точками. Расстояние от точки до плоскости и между плоскостями в евклидовом аффинном пространстве.
Домашнее задание:
- 49.20бв, 51.2аг, 51.6а, 51.7в, 51.8, 51.14б, 51.15.
11 мая 2018
Аффинные отображения, достаточное условие наличия неподвижных точек. Движения евклидовых пространств, вектор скольжения. Классификация движений в размерностях 2 и 3, задача на геометрическое описание движения 2-мерной плоскости.
Домашнее задание:
- 49.27а, 49.28, 51.19, 51.20, 51.21, 51.23аб, 51.24авг.
16 мая 2018
Задача на геометрическое описание движения 3-мерного пространства.
Квадратичные функции на аффинном пространстве, их координатная запись, расширенная матрица квадратичной функции. Квадратичные гиперповерхности (квадрики). Приведение квадратичной функции (квадрики) к каноническому или к нормальному виду и к главным осям. Различные типы квадрик (центральные и нецентральные, конические и неконические). Центр квадратичной функции (квадрики), его нахождение.
Домашнее задание:
- 52.4, 52.6авг, 52.16, 52.17, 52.19а, 52.20б, 52.21бв, 52.22суф.
18 мая 2018
Тензоры, примеры: тензоры малых валентностей, det. Операции над тензорами: сложение, умножение на скаляры, тензорное умножение. Компоненты тензора, тензорный базис, правило Эйнштейна. Операции над тензорами в координатах, разложимые тензоры. Преобразование компонент тензора при замене координат.
Домашнее задание:
- 47.1бв, 47.2, 47.3б, 47.4, 47.7ав;
- ★ тензор det нельзя разложить в произведение тензоров меньших валентностей.
23 мая 2018
Свёртка тензора. Выражение различных операций линейной алгебры в терминах тензорного произведения и свёртки. Ковариантные и контравариантные тензоры, симметрические и кососимметрические тензоры, симметризация и альтернирование. Внешнее умножение внешних форм, его свойства, связь с определителями. Базис и размерность пространства внешних форм. Канонический вид кососимметрической билинейной функции, приведение к каноническому виду с помощью внешнего умножения (аналог метода Лагранжа).
Домашнее задание:
- 47.9, 47.13б, 47.14, 48.14, 48.16, 37.33вг.
25 мая 2017
Контрольная работа
- Ортогонализация системы векторов (1 вариант); вычисление объёма параллелепипеда (2 вариант).
- Нахождение угла между вектором и подпространством (1 вариант); вычисление расстояния от точки до плоскости (2 вариант).
- Приведение симметрической билинейной формы (1 вариант) и квадратичной формы (2 вариант) к главным осям.
- Определение типа движения плоскости (1 вариант) и пространства (2 вариант) и его полное геометрическое описание.
- Полярное разложение невырожденного линейного оператора.