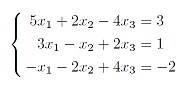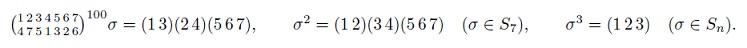Преподаватель: Д.А.Тимашёв

Занятия проходят в ауд. 404 по средам на каждой чётной неделе на 3-й паре (13:15-14:50) и по пятницам на 2-й паре (10:45-12:20).

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.

Системы линейных уравнений (СЛУ), их матрицы, элементарные преобразования. Решение СЛУ методом Гаусса.

• 8.1вг, 8.2а, 8.7.

Задача о полиномиальной интерполяции. Метод Крамера решения квадратных СЛУ малых размеров (2×2 и 3×3). Определители 2-го и 3-го порядка.

• 8.2вг, 8.6вд, 8.8, 9.1гд, 9.2ж, 16.1б;
• решить методом Крамера систему линейных уравнений:
• ;
• ★ найти явную формулу для интерполяционного многочлена.

Арифметическое векторное пространство R^n. Линейная зависимость, базис системы векторов, координаты вектора в базисе. Стандартный базис в R^n.

• 6.4, 6.11, 6.13, 6.14.

Алгоритм нахождения базиса конечной системы векторов в R^n. Ранг матрицы, его вычисление.

• 6.12вги, 7.1дл, 7.2аз, 7.5, 7.7, 7.10.

Ранг суммы матриц. Пространство решений ОСЛУ, фундаментальная система решений.

• 8.4бвг, 8.25★.

Элементы комбинаторики: число размещений, перестановок, сочетаний. Бином Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля. Подстановки: двухрядная запись, умножение, циклические подстановки, разложение на независимые циклы.

• 2.11вгдж, 2.13, 3.1вг, 3.2аге.

Возведение подстановок в степень. Решение уравнений в подстановках.

Чётность и знак подстановок. Знак цикла. Задача про «пятнашки»: можно ли, последовательно передвигая фишки на соседнее свободное место, поменять местами фишки 14 и 15, оставив остальные фишки на месте?

• 3.6бвж, 3.11, 3.13, 3.22бв;
• решить уравнения в подстановках:
• 
• можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы угловые кубики одной из граней переставились по кругу, а остальные кубики остались на своих местах (возможно, повернувшись)?

Определители квадратных матриц, их вычисление по развёрнутой формуле. Свойства определителя, его поведение при различных преобразованиях матрицы. Вычисление определителей приведением к треугольному виду.

• 10.4б, 16.2, 11.1вгд, 11.4, 13.1бвж.

Вычисление определителей приведением к треугольному виду и приведением к определителю Вандермонда. Определитель с углом нулей. Разложение определителя по строке и столбцу.

• 13.2ежз, 14.1зкм★, 12.2, 12.3ези.

Трёхдиагональные определители и линейные однородные рекуррентные уравнения 2-го порядка.

• 14.1где, 12.4, 4.5;
• вычислить определитель:
• 

Арифметические операции над матрицами (сложение матриц, умножение матриц на числа, умножение матриц), их свойства, некоммутативность умножения матриц, умножение на диагональные матрицы.

• 17.1бв, 17.4ав, 17.25.

Единичная матрица. Элементарные матрицы, умножение на них слева и справа. Обратная матрица, её единственность и критерий существования. Явная формула для обратной матрицы. Решение матричных уравнений вида AX=B и нахождение обратной матрицы с помощью решения уравнения AX=E.

• 18.3взи, 18.8гкл, 18.9кл, 18.17★, 19.3абв.

Определитель произведения матриц. Ранг произведения матриц, случай невырожденности одного из сомножителей. Ранг присоединённой матрицы.

• 15.2бвг, 16.19, 7.11, 16.4;
• найти rk Ǎ, если rk A = n-1, где n — размер квадратной матрицы A.

1. Решение СЛУ в зависимости от параметра.
2. Нахождение ФСР и размерности пространства решений ОСЛУ (1 вариант); нахождение базиса системы векторов и выражение через него остальных векторов системы (2 вариант).
3. Решение матричного уравнения (1 вариант); нахождение обратной матрицы (2 вариант).
4. Вычисление определителя размера 4×4.
5. Вычисление определителя размера n×n.
6. Вычисление трёхдиагонального определителя (1 вариант); решение уравнения в подстановках (2 вариант).

Поле комплексных чисел. Вычисления над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, решение алгебраических задач геометрическими методами (пример: уравнение |(z+1-i)/(z-1+i)|=1) и геометрических задач методами алгебры комплексных чисел (пример: доказательство теоремы о том, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон).

Тригонометрическая форма записи комплексных чисел, формула Муавра, вычисления над комплексными числами в тригонометрической форме. Выражение тригонометрических функций кратных углов через функции исходного угла и степеней тригонометрических функций через функции кратных углов в первой степени с помощью комплексных чисел.

• 20.1еж, 21.2бж, 21.9аг, 21.10, 21.12, 21.13г;
• доказать с помощью комплексных чисел теорему Птолемея: произведение диагоналей четырёхугольника, вписанного в окружность, равно сумме произведений его противоположных сторон.