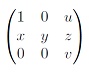Кафедра высшей алгебры

Преподаватель: Д.А. Тимашёв

Занятия проходят по понедельникам на каждой нечётной неделе на 1-й паре (9:00-10:35) в ауд. 14-14 и по средам на каждой чётной неделе на 2-й паре (10:45-12:20) в ауд. 406.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И. Кострикина, новое изд., Москва, МЦНМО, 2009. Дополнительные задачи помечены знаком ★.

Группы (напоминание из 1-го семестра): определение, единственность нейтрального и обратного элементов в группе, абелевы группы, мультипликативная и аддитивная терминологии. Примеры групп: аддитивные и мультипликативные группы колец и полей, матричные и линейные группы, группы движений (в т.ч. группа диэдра D_n), группы подстановок (симметрическая группа S_n и знакопеременная группа A_n). Задание конечной группы таблицей умножения, примеры: группа Клейна V₄ и группа кватернионов Q₈. Изоморфизм групп, примеры изоморфных и неизоморфных групп: аддитивная и мультипликативная группы поля R, а также группа положительных вещественных чисел по умножению; Z₆, S₃ и D₃; Z₄ и V₄. Порядок элемента группы, его свойства, циклические подгруппы.

• 55.16, 55.25абг, 55.26, 56.7, 56.10, 56.11;
• какие из групп изоморфны: аддитивная группа поля рациональных чисел, его мультипликтивная группа, группа положительных рациональных чисел (по умножению)?
• изоморфны ли группы GL₂(C) и GL₃(C)?

Теорема Лагранжа и её следствия о порядках элементов в конечных группах. Проблема классификации конечных групп, группы простого порядка. Сопряжённость элементов в группе, классы сопряжённости, центр группы. Вычисление классов сопряженности и центра для групп Q₈, S_n, D_n.

• доказать, что любая группа порядка 4 изоморфна либо Z₄ либо V₄;
• ★ доказать, что любая группа порядка 6 изоморфна либо Z₆ либо S₃;
• 57.29, 57.30б, 57.36, 58.20бв, 58.23, 58.24агж.

Нормальные подгруппы, их перечисление в группах S₃, S₄. Факторгруппы. Основная теорема о гомоморфизмах, вычисление факторгрупп с её помощью.

• 58.1абд, 58.3, 58.4б, 58.10, 58.11а, 58.32бде, 58.33аге, 58.39.

Автоморфизмы групп, группа автоморфизмов циклической группы, вычисление Aut(Aut(Aut Z₉)). Группа внутренних автоморфизмов Inn(G), её нормальность в Aut(G). Прямое произведение (прямая сумма) групп, примеры разложений и неразложимости групп в прямые произведения (прямые суммы).

• 57.39а, 57.40, 57.41б, 58.43, 60.1, 60.2бг, 60.7, 60.8;
• ★ доказать, что Aut(S_n) = Inn(S_n), кроме случая n=6.

Системы порождающих в группе, конечно порождённые и не конечно порождённые группы, примеры. Случай абелевых групп, свободные конечно порождённые группы. Структура конечно порождённых абелевых групп, её определение, исходя из представления группы в виде факторгруппы свободной группы по подгруппе, заданной набором порождающих элементов, приведением целочисленной матрицы координат порождающих элементов подгруппы к «диагональному» виду. Вычисление порядка элемента в конечно порождённой абелевой группе, представленной как факторгруппа свободной группы.

• 60.32, 60.50, 60.51, 60.52агд, 60.53.
• Доказать:
  1. группа S_n порождена транспозицией (1,2) и циклом (1,2,…,n);
  2. группа A_n порождена парами независимых транспозиций при n ≥ 5;
  3. группа B_n(K) невырожденных верхнетреугольных матриц порождена элементарными матрицами 1-го и 3-го типов.
• Являются ли конечно порождёнными следующие группы:
  1. группа рациональных дробей m/n, у которых простые делители n содержатся среди {p₁,…,p_s}, с операцией сложения;
  2. группа рациональных дробей m/n≠0, у которых простые делители m и n содержатся среди {p₁,…,p_s}, с операцией умножения.

Объём целочисленного параллелепипеда. Конечные абелевы группы, их структура, тип группы. Классификация конечных абелевых групп заданного порядка. Определение типа факторгруппы конечной (или конечно порождённой) абелевой группы. Вложимость конечных абелевых групп друг в друга.

• 60.5в, 60.39ежз, 60.40ав, 60.42, 60.43а;
• доказать, что группу Z_p^k нельзя разложить в прямую сумму нетривиальных подгрупп;
• доказать формулу для объёма целочисленного n-мерного параллелепипеда П:
  • vol(П) = ∑ (1/2^k)⋅(число целых точек внутри всех (n-k)-мерных граней П), где суммирование ведётся по k=0,1,…,n;
• доказать формулу Пика для площади целочисленного многоугольника P:
  • S(P) = (число целых точек внутри P) + ½ · (число целых точек на границе P) - 1.

Количество подгрупп заданного порядка в данной конечной абелевой группе. Действия групп на множествах, описание орбит и стабилизаторов. Порядок орбиты конечной группы.

• 60.43бв, 57.1бв, 57.2, 57.3, 57.9бв, 57.10в, 57.12аб;
• доказать, что стабилизаторы разных точек из одной орбиты сопряжены друг другу.

Правильные многогранники, их классификация и группы движений. Действие группы на себе сопряжениями: классы сопряжённости и централизаторы, число элементов в классе сопряжённости, формула классов.

• 57.13в★, 57.23б, 57.25, 57.28, 57.31, 58.35, 58.44;
• ★ перечислить с точностью до изоморфизма все группы порядка p³ (p — простое число).

Коммутант группы, его свойства. Вычисление коммутанта группы G методом оценки сверху (ядро гомоморфизма G в абелеву группу) и снизу (подгруппа, порождённая некоторым количеством коммутаторов). Кратные коммутанты, разрешимые группы, критерий разрешимости (в терминах подгруппы и факторгруппы).

• 62.7бг, 62.8б, 62.10, 62.11в, 62.13, 62.20;
• вычислить производный ряд для группы, состоящей из невырожденных действительных матриц вида
• 

Силовские подгруппы, теоремы Силова, примеры: силовские подгруппы в A₄, в SL₂(Z_p), в прямом произведении групп.

• 59.3а, 59.4а, 59.9, 59.11, 59.13где, 59.14, 59.15;
• описать все силовские 3-подгруппы в D₃×A₄.

Коллоквиум

Арифметика конечных групп: доказательство непростоты, разрешимости и коммутативности групп заданного порядка. Полупрямое произведение групп, пример: D_n. Классификация групп порядка ≤10.

• 59.20вг, 59.22ав, 59.23, 59.24, 62.18вгде★, 62.22★, 62.23★;
• какие из групп в задаче 60.2 разложимы (нетривиальным образом) в полупрямое произведение?
• доказать, что любая неабелева группа порядка 8 изоморфна либо Q₈, либо D₄.

Линейные и матричные представления групп, в том числе мономиальное представление симметрической группы и представление в пространстве функций на множестве с действием группы. Приводимые, неприводимые и вполне приводимые представления, разложение в прямую сумму неприводимых представлений. Теорема Машке. Описание неприводимых комплексных представлений конечных абелевых групп (пример: V₄). Описание одномерных комплексных представлений конечных групп (примеры: S_n, S₃×D₅).

• 69.2, 69.6, 69.7, 69.9, 69.11, 70.2жз, 70.10;
• описать все одномерные комплексные представления группы A₄×D₄.

Факты о количестве и размерностях неприводимых комплексных представлений конечной группы. Описание всех неприводимых комплексных представлений группы D_n.

Кольца, алгебры, идеалы, факторкольца и факторалгебры. Факторалгебры K[x]/p·K[x], их свойства, вычисления в K[x]/p·K[x]. Присоединение корня, избавление от иррациональности в знаменателе.

• 70.34е, 70.37аб, 70.39, 63.21, 64.8, 64.43;
• описать все неприводимые комплексные представления групп Q₈ и A₄.
• представить выражение (a²-3a-1)/(a²+2a+1) в виде многочлена от a наименьшей возможной степени с рациональными коэффициентами, где a∈C — корень многочлена x³+x²+3x+4.

1. Вычисление факторгруппы свободной абелевой группы и нахождение в ней количества элементов заданного порядка (1 вариант) и порядка заданного элемента (2 вариант).
2. Нахождение централизатора элемента группы подстановок и количества элементов в его классе сопряжённости (1 вариант); описание орбит действия группы на множестве (2 вариант).
3. Доказательство коммутативности группы заданного порядка (1 вариант); описание силовских подгрупп в группе (2 вариант).
4. Вычисление производного ряда группы (1 вариант); доказательство разрешимости группы заданного порядка (2 вариант).
5. Описание одномерных комплексных представлений группы.
6. Избавление от иррациональности в знаменателе выражения в поле, получаемом присоединением корня неприводимого многочлена к полю Z₂ (1 вариант) и Q (2 вариант).