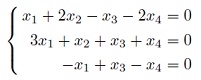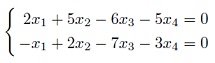Кафедра высшей алгебры

Преподаватель: Д.А.Тимашёв

Занятия проходят по понедельникам c 18:30 по 21:50 в ауд. 13-03.

1. Векторные пространства, базисы, размерность, координаты. Правило замены координат.
2. Подпространства, операции над ними, взаимное расположение подпространств.
3. Линейные функции, сопряжённое пространство.
4. Линейные отображения и линейные операторы.
5. Собственные векторы и собственные значения линейного оператора. Теория жордановой нормальной формы.
6. Билинейные функции (симметрические и кососимметрические). Квадратичные формы.
7. Евклидовы векторные пространства, их геометрия.
8. Операторы в евклидовых пространствах: ортогональные, симметрические. Полярное разложение.
9. Тензоры.

1. А.И.Кострикин. Введение в алгебру. Часть II. Линейная алгебра.
2. Э.Б.Винберг. Курс алгебры. Главы 5−8.
3. А.И.Кострикин, Ю.И.Манин. Линейная алгебра и геометрия.
4. Сборник задач по алгебре под ред. А.И.Кострикина. Часть II. Линейная алгебра и геометрия.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2001. Дополнительные задачи помечены знаком ★.

Векторные пространства над произвольным полем K, скаляры и векторы, примеры: арифметическое пространство K^n, геометрические векторы, пространство матриц, пространство функций на множестве, пространство многочленов, расширения полей. Простейшие следствия аксиом векторного пространства.

Линейные комбинации векторов, линейная зависимость, основная лемма о линейной зависимости.

Базис и размерность векторного пространства, координаты вектора в базисе. Конечномерные и бесконечномерные векторные пространства.

Изоморфизм векторных пространств. Любое векторное пространство размерности n<∞ над полем K изоморфно арифметическому пространству K^n.

Матрица перехода от одного базиса к другому, её свойства. Правило преобразования координат вектора при замене базиса.

Экзотический пример векторного пространства: множество всех подмножеств множества X с операцией симметрической разности подмножеств — векторное пространство над полем Z_2. Линейная независимость системы функций 1, cos(x), … , cos(nx) в пространстве функций на вещественной прямой (34.3г). Преобразование координат вектора при замене базиса (34.10а).

• 34.7а, 34.4б, 34.10в, 34.11а, 34.8бвд★;
• доказать, что множество R^+ положительных чисел с операциями u⊕v = u·v (u,v∈R^+) и λ⊗v = v^λ (λ∈R, v∈R^+) является векторным пространством над полем R, и найти его размерность.

Подпространства в векторном пространстве, примеры и конструкции подпространств: линейная оболочка множества векторов, пространство решений однородной системы линейных уравнений, пересечение подпространств. Объединение подпространств — вообще говоря, не подпространство. Сумма подпространств.

Подпространство конечномерного векторного пространства конечномерно, его размерность не превосходит размерности пространства и строго меньше для собственного подпространства. Базис пространства, согласованный с подпространством. Существование базиса конечномерного пространства, согласованного с парой подпространств, их суммой и пересечением. Формула Грассмана для размерности суммы двух подпространств. Нетривиальность пересечения двух подпространств, сумма размерностей которых больше размерности пространства.

Линейная независимость подпространств, прямая сумма подпространств, проекции вектора на прямые слагаемые. Примеры: разложение пространства геометрических векторов в прямую сумму плоскости и прямой, разложение конечномерного векторного пространства в прямую сумму координатных осей, разложение пространства квадратных матриц в прямую сумму подпространств симметрических и кососимметрических матриц. Размерность и базис прямой суммы подпространств.

Примеры подпространств (35.3ге). Векторные пространства над конечным полем (35.10аб).

• 35.3джз, 35.9, 35.10вгде.

Линейные функции на векторном пространстве V: определение, примеры (след матрицы, вычисление значения функции в точке множества), запись в координатах на конечномерном пространстве (линейные формы). Сопряжённое (двойственное, дуальное) пространство V*, его размерность. Сопряжённый (двойственный, дуальный) базис пространства V*. Канонический изоморфизм пространств V и (V*)* в конечномерном случае. Двойственность между векторами и линейными функциями (ковекторами).

Аннулятор подмножества в векторном пространстве, его свойства. Размерность аннулятора, совпадение второго аннулятора подпространства с этим подпространством в конечномерном случае. Любое подпространство в конечномерном векторном пространстве задаётся однородной системой линейных уравнений (ОСЛУ). Критерий базисности набора линейных функций: задаваемая ими квадратная ОСЛУ имеет только нулевое решение. Интерполяционная формула Лагранжа как разложение многочлена по базису в терминах сопряжённого базиса.

Применения формулы Грассмана: 7-мерное подпространство пространства матриц размера 4×4 содержит ненулевую треугольную матрицу. Прямая сумма подпространств: недостаточность условия нулевых попарных пересечений подпространств, разложение в прямую сумму (35.18). Ядро линейной функции (36.13а).

• 35.19, 35.22, 36.13б, 36.14;
• если матрица A размера n×n имеет ранг ≤n/2, то матричное уравнение AX=0 имеет решением ненулевую симметрическую матрицу X.

Линейные отображения векторных пространств: определение, примеры (линейные функции, поворот плоскости, проекция пространства на плоскость, транспонирование матриц, дифференцирование функций). Матрица линейного отображения: определение, примеры (матрицы поворота плоскости и проекции пространства на плоскость), запись линейного отображения в координатах. Взаимно однозначное соответствие между линейными отображениями и матрицами (при выборе базисов). Преобразование матрицы линейного отображения при замене базисов. Операции над линейными отображениями и соответствующие операции над матрицами (сложение, умножение на скаляр, произведение).

Образ и ядро линейного отображения. Критерии инъективности/сюръективности/биективности линейного отображения в терминах ядра и образа. Размерность ядра и образа, ранг линейного отображения. Новое доказательство теоремы о размерности пространства решений ОСЛУ. Геометрическая структура линейного отображения: подпространство, дополнительное к ядру, изоморфно отображается на образ.

Задание подпространства однородной системой линейных уравнений ⇔ нахождение аннулятора подпространства (35.16а).

• 35.16б.

Линейные операторы на векторном пространстве (пример: единичный оператор). Матрица линейного оператора, её преобразование при замене базиса. Алгебра линейных операторов, её изоморфизм с алгеброй квадратных матриц.

Определитель и след линейного оператора, их независимость от выбора базиса. Невырожденные линейные операторы, эквивалентные условия невырожденности.

Инвариантные подпространства для линейного оператора, вид матрицы оператора в базисе, согласованном с инвариантными подпространствами.

Собственные векторы и собственные значения линейного оператора. Характеристический многочлен. Наличие собственных векторов у линейного оператора в комплексном векторном пространстве. Собственные подпространства, их линейная независимость. Алгебраическая и геометрическая кратности собственного значения. Диагонализуемые операторы, эквивалентные условия диагонализуемости. Операторы с простым спектром диагонализуемы.

Нахождение базиса и системы линейных уравнений для суммы и пересечения подпространств (35.15г).

• 35.15в;
• Задать системой однородных линейных уравнений сумму подпространств U+W в 4-мерном пространстве V при условии, что подпространства U и W заданы с помощью ОСЛУ:
• 

Подстановка линейного оператора или матрицы в многочлен. Теорема Гамильтона–Кэли (для линейных операторов в конечномерном комплексном векторном пространстве). Существование инвариантного подпространства размерности ≤2 для линейного оператора в конечномерном вещественном векторном пространстве.

Корневые векторы линейного оператора (пример: собственные и корневые векторы оператора дифференцирования в пространстве функций на прямой). Корневые подпространства, их свойства: инвариантность, размерность равна алгебраической кратности собственного значения, ограничение оператора на корневое подпространство. Линейная независимость корневых подпространств, разложение векторного пространства в прямую сумму корневых подпространств.

Нахождение матрицы линейного оператора (39.15вл), её преобразование при замене базиса (39.20).

• 39.15ен, 39.19.

Циклические подпространства для нильпотентного линейного оператора (пример: циклические подпространства оператора дифференцирования в пространстве многочленов), их свойства: инвариантность, базис и размерность, матрица нильпотентного оператора на циклическом подпространстве — нильпотентная жорданова клетка. Разложение векторного пространства в прямую сумму циклических подпространств, жорданов базис и жорданова нормальная форма для нильпотентного оператора. Графическое изображение действия нильпотентного оператора на жордановом базисе с помощью диаграммы Юнга.

Жорданова нормальная форма (ЖНФ) и жорданов базис (ЖБ) для линейного оператора в комплексном векторном пространстве: существование, единственность ЖНФ с точностью до перестановки жордановых клеток, формулы для количества клеток с заданным собственным значением (всех и данного размера).

Вычисление коэффициентов характеристического многочлена (40.10). Вычисление собственных значений и нахождение собственных векторов (40.15е). Диагонализумость линейных операторов (40.16а).

• 40.7, 40.9, 40.15бг, 40.16вг.

Билинейные функции на векторных пространствах: определение, примеры (скалярное произведение геометрических векторов, определитель матрицы 2×2 как билинейная функция столбцов, след произведения матриц, интеграл произведения функций). Запись билинейных функций в координатах (билинейные формы), матрица билинейной функции, её преобразование при замене базиса. Ранг билинейной функции, невырожденные билинейные функции. Линейное отображение в сопряжённое пространство, задаваемое билинейной функцией, его матрица и критерий биективности.

Симметрические и кососимметрические билинейные функции, примеры. Ортогональное дополнение к подпространству относительно симметрической или кососимметрической билинейной функции, его свойства, связь с аннулятором.

Квадратичные функции на векторном пространстве, ассоциированные с симметрическими билинейными функциями, их запись в координатах (квадратичные формы). Восстановление симметрической билинейной функции по ассоциированной квадратичной функции (формула поляризации). Канонический вид симметрических билинейных и квадратичных функций, алгоритм Лагранжа приведения к каноническому виду.

Сумма и произведение собственных значений линейного оператора. Нахождение ЖНФ и ЖБ (41.1е).

• 41.1км, 41.10вг, 41.7, 41.30.

Угловые миноры матрицы симметрической билинейной (или квадратичной) функции, метод Якоби приведения к каноническому виду. Нормальный вид симметрических билинейных и квадратичных функций над полями C и R. Сигнатура и индексы инерции квадратичной функции над R, закон инерции. Положительно определённые симметрические билинейные и квадратичные функции, критерий Сильвестра.

Евклидовы векторные пространства: определение, примеры (геометрические векторы, R^n со стандартным скалярным умножением, конечномерные подпространства в пространстве непрерывных функций на отрезке). Изоморфизм евклидовых пространств. Все евклидовы пространства одной размерности изоморфны друг другу.

Приведение квадратичной функции к каноническому виду алгоритмом Лагранжа (38.18а). Приведение симметрической билинейной функции к каноническому виду методом Якоби (38.8б). Эквивалентность квадратичных форм над R (38.17а).

• 38.18вгз, 38.8а, 38.17б, 38.19а.

Длина вектора в евклидовом пространстве, её простейшие свойства. Неравенство Коши–Буняковского. Неравенство треугольника. Угол между векторами.

Ортогональность векторов в евклидовом пространстве. Обобщённая теорема Пифагора. Ортогональные и ортонормированные базисы, ортогональные системы координат. Ортогональные матрицы, их характеризация как матриц перехода от одного ортонормированного базиса к другому.

Ортогональное дополнение к подпространству в евклиловом пространстве, его свойства. Ортогональная проекция и ортогональная составляющая вектора относительно подпространства. Процесс ортогонализации Грама–Шмидта (пример: многочлены Лежандра).

Матрица и определитель Грама, их свойства. Расстояние между векторами в евклидовом пространстве, его свойства.

При каких значениях параметра квадратичная функция положительно определена (38.11б). Нахождение ортогональной проекции и ортогональной составляющей вектора (43.19а). Ортогонализация системы векторов (43.15а).

• 38.11в, 38.14а, 43.19б, 43.15б.

Расстояние и угол между вектором и подпространством достигаются на ортогональной проекции вектора. Формула для расстояния от вектора до подпространства в терминах определителей Грама. Объём многомерного параллелепипеда в евклидовом пространстве: индуктивное определение, выражение через определитель Грама и через определитель матрицы координат порождающих векторов в ортонормированном базисе.

Взаимно однозначное соответствие между линейными операторами и билинейными функциями на евклидовом пространстве. Сопряжённый оператор, его матрица в ортонормированном базисе.

Оператор, сопряжённый к произведению операторов. Ортогональное дополнение к инвариантному подпространству инвариантно относительно сопряжённого оператора.

Ортогональные операторы, эквивалентные условия ортогональности, примеры: поворот плоскости и осевая симметрия.

Нахождение расстояния и угла между вектором и подпространством (43.38б). Вычисление объёма параллелепипеда (43.36б). Линейная независимость системы векторов с попарными углами π/3 (43.39).

• 43.38а, 43.21б, 43.40, 43.45а (при n=3).

Канонический вид матрицы ортогонального оператора.

Симметрические (самосопряжённые) операторы. Наличие собственного вектора у симметрического оператора. Канонический вид матрицы симметрического оператора. Приведение симметрических билинейных и квадратичных функций к главным осям. Неотрицательные и положительно определённые симметрические операторы, пример: A*·A, где A — произвольный оператор. Критерий неотрицательности и положительной определённости симметрического оператора в терминах собственных значений. Извлечение квадратного корня из неотрицательного и положительно определённого оператора.

Полярное разложение невырожденного линейного оператора в евклидовом пространстве.

Собственные значения ортогонального или симметрического оператора, ортогональность собственных подпространств. Приведение ортогонального оператора к каноническому виду (46.6в).

• 46.6гж, 46.14.

Тензоры: определение, примеры тензоров малых валентностей (скаляры, ковекторы, векторы, билинейные функции, сопоставление линейному оператору тензора типа (1,1)), определитель как тензор типа (n,0). Операции над тензорами: сложение, умножение на скаляры, тензорное умножение, их свойства.

Тензорный базис пространства тензоров типа (p,q), его размерность. Компоненты тензора, их преобразование при замене координат в основном пространстве. Правило Эйнштейна. Операции над тензорами в координатах. Изоморфизм пространств линейных операторов и тензоров типа (1,1) над основным пространством.

Свёртка тензора по паре индексов, её действие на вполне разложимых тензорах, компоненты свёрнутого тензора. Свёртка по нескольким парам индексов.

Приведение квадратичной функции к главным осям (45.19и).

• 45.19е, 45.4г, 45.14.

Примеры свёртки (спаривание вектора с ковектором, значение билинейной функции на паре векторов, след линейного оператора, применение оператора к вектору, произведение линейных операторов).

Ковариантные и контравариантные тензоры. Симметрические и кососимметрические тензоры. Операции симметризации и альтернирования тензоров, их свойства.

Внешнее умножение кососимметрических тензоров, его свойства: антикоммутативность, ассоциативность, внешнее произведение ковекторов и определители. Базис и размерность пространства кососимметрических тензоров данной валентности.

Полярное разложение линейного оператора.

• 46.16бв (полярное разложение в обоих порядках).

27 мая, 18:30, ауд. 13-03.

• 3 июня, 18:30, ауд. 13-03;
• 5 июня, 18:30, ауд. 13-03.