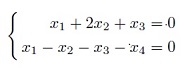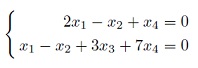Кафедра высшей алгебры

Преподаватель: Д.А.Тимашёв

Занятия проходят по понедельникам и четвергам на 4-й паре (15:00-16:35) в ауд. 407.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, новое изд., Москва, МЦНМО, 2009. Дополнительные задачи помечены знаком ★.

Векторные пространства: простейшие следствия из аксиом, примеры (в частности: множество 2^X всех подмножеств множества X как векторное пространство над Z₂, абелеву группу Z нельзя превратить в векторное пространство). Изоморфизм векторных пространств (пример: 2^X ≅ {функции X→Z₂}). Линейные комбинации векторов, линейная зависимость, примеры линейно независимых систем функций. Базис, размерность, координаты. Изоморфизм конечномерного векторного пространства с арифметическим. Расширения полей как векторные пространства, число элементов конечного поля.

• 34.3дж, 34.4б, 34.5, 34.7бг, 34.8гд★з, 35.10абвг;
• доказать, что множество R⁺ положительных чисел с операциями u⊕v = u·v (u,v∈R⁺) и λ⊗v = v^λ (λ∈R, v∈R⁺) является векторным пространством над полем R.

Дополнение линейно независимой системы векторов до базиса. Матрица перехода к другому базису, её свойства, преобразование координат вектора при замене базиса. Подпространства, примеры. Базис, согласованный с подпространством.

• 34.10в, 34.11а, 34.12, 34.14аг, 35.3вдеж, 35.9, 35.10.

Пересечение и сумма двух подпространств (объединение — вообще говоря, не подпространство). Базис, согласованный с парой подпространств, формула Грассмана для размерности их суммы (пример: 7-мерное подпространство пространства матриц размера 4×4 содержит ненулевую симметрическую матрицу). Инварианты взаимного расположения пары подпространств, обсуждение инвариантов троек подпространств. Прямая сумма подпространств, проекции на прямые слагаемые (пример: разложение пространства квадратных матриц в прямую сумму подпространств симметрических и кососимметрических матриц).

• 35.17, 35.18, 35.22, 35.24, 35.26, 35.27.
• Если матрица A размера n×n имеет ранг ≤ n/2, то матричное уравнение AX=0 имеет решением ненулевую треугольную матрицу X.
• ★ Найти полную систему инвариантов взаимного расположения трёх подпространств в конечномерном векторном пространстве. Какое минимальное количество инвариантов для этого необходимо?
• Показать на примере, что для задания взаимного расположения четвёрки подпространств с точностью до изоморфизма недостаточно дискретных инвариантов (размерностей самих подпространств, их сумм, пересечений, …).

Линейные функции на векторном пространстве V, их координатная запись. Ядро линейной функции. Сопряжённое пространство V*, сопряжённый базис. Канонический изоморфизм пространств V и (V*)* в конечномерном случае. Двойственность между векторами и линейными функциями (ковекторами). Критерий базисности набора ковекторов, применение: интерполяционная формула Лагранжа.

• 36.9в, 36.14, 36.16, 36.18, 36.20;
• доказать, что набор линейных функций (β₀, …, β_n) на пространстве V многочленов степени ≤ n над полем K зарактеристики 0, где β_i(f) равно значению i-й производной многочлена f в точке t₀ ∈ K, образует базис пространства V*, найти сопряжённый ему базис в пространстве V и разложение произвольного многочлена f ∈ V по этому базису;
• (кратная интерполяция) доказать, что для любого набора попарно различных точек x₁, …, x_k на действительной прямой, любого набора натуральных чисел n₁, …, n_k и любого набора значений y_ij (1≤i≤k, 0≤j<n_i) существует единственный многочлен f степени < n₁+…+n_k, у которого значение j-й производной в точке x_i равно y_ij (при всех возможных i,j).

Аннулятор подпространства, его размерность. Совпадение второго аннулятора подпространства с этим подпространством в конечномерном случае. Задание подпространства однородной системой линейных уравнений ⇔ нахождение базиса аннулятора подпространства. Нахождение суммы и пересечения подпространств.

Линейные отображения, их матрицы, запись линейного отображения в координатах. Преобразование матрицы линейного отображения при замене базисов.

• 35.15в, 35.16б, 35.25, 36.2, 36.3, 36.4;
• задать системой однородных линейных уравнений сумму подпространств U+W в 4-мерном пространстве V при условии, что подпространства U и W заданы с помощью ОСЛУ:
• и