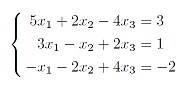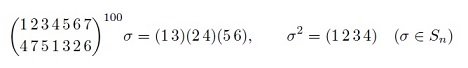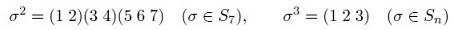Кафедра высшей алгебры

Преподаватель: Д.А.Тимашёв

Занятия проходят на 3-й паре (13:15-14:50) по понедельникам на каждой чётной неделе в ауд. 406 и по четвергам в ауд. 14-15.

Объявления:

• Семинар с четверга 28 ноября переносится на субботу 14 декабря, 3-я пара (13:15-14:50), ауд. 413.
• Контрольная работа по алгебре пройдёт на семинаре в понедельник 16 декабря.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, новое изд., Москва, МЦНМО, 2009. Дополнительные задачи помечены знаком ★.

Системы линейных уравнений (СЛУ). Метод Крамера решения квадратных СЛУ малых размеров (2×2 и 3×3). Определители 2-го и 3-го порядка.

• 8.6вд, 8.2е, 9.1гд, 9.2ж, 16.1а;
• решить методом Крамера систему линейных уравнений:
• 

Элементарные преобразования СЛУ и их матриц. Метод Гаусса решения СЛУ. Критерий совместности и определённости квадратной СЛУ: ассоциированная ОСЛУ должна быть определена.

• 8.1вг, 8.2вг, 8.8;
• доказать теорему о полиномиальной интерполяции: для любого набора n различных точек x₁, … , x_n и любого набора n (не обязательно различных) значений y₁, … , y_n существует единственный многочлен f(x) степени < n, принимающий в точках x_i значения y_i.

Арифметическое векторное пространство Rⁿ. Линейная зависимость и базис системы векторов.

• 6.4, 6.6, 6.7вд, 6.9абд; 6.13, 6.14;
• найти явную формулу для интерполяционного многочлена;
• доказать, что для подсистемы векторов B⊂S следующие условия эквивалентны:
  1. B линейно независима и линейно порождает систему S;
  2. B — минимальная (по включению) порождающая подсистема в S.

Ранг системы векторов. Координаты вектора в базисе. Стандартный базис в Rⁿ. Алгоритм нахождения базиса конечной системы векторов в Rⁿ. Ранг матрицы, его свойства.

• 6.12вги, 6.14, 7.1дл, 7.2аж, 7.3, 7.5, 7.19★.

Вычисление ранга матрицы. Подпространства в Rⁿ, примеры: линейная оболочка системы векторов, пространство решений ОСЛУ. Фундаментальная система решений ОСЛУ, её нахождение.

• 7.2з, 7.7, 7.10, 8.4бвг, 8.25★.

Алгебраические операции над матрицами, их свойства, нулевая и единичная матрицы. Некоммутативность умножения матриц, делители нуля и нильпотентные матрицы, нильпотентность нильтреугольных матриц. Умножение на диагональные матрицы и на матричные единицы.

• 17.1бв, 17.4ав, 17.13, 17.25, 17.26★, 19.4абв, 19.15;
• доказать, что квадратная матрица A, коммутирующая со всеми квадратными матрицами B того же размера (т.е. A·B = B·A), имеет вид A = λ·E для некоторого числа λ.

Элементарные матрицы, умножение на них слева и справа. Обратная матрица. Если матрица N нильпотентна, то матрицы E+N и E-N обратимы. Решение матричных уравнений вида AX=B. Нахождение обратной матрицы.

• 17.18, 18.3взи, 18.4, 18.9дкл, 18.17★, 19.3бв, 19.14, 19.21;
• решить матричное уравнение:
• 

Обратная матрица к произведению матриц, к транспонированной матрице. Задача: как изменится A^-1, если записать строки матрицы A в обратном порядке?

Перестановки и подстановки, их количество. Умножение подстановок. Циклические подстановки, разложение произвольной подстановки на независимые циклы, применение к возведению подстановок в степень.

• 3.1вг, 3.2аге, 3.3ав, 3.13;
• как изменится A^-1, если матрицу A подвергнуть одному из следующих преобразований:
  • транспонировать относительно побочной диагонали;
  • повернуть на 90º против часовой стрелки?
• решить уравнения в подстановках:
  • 
• (задача о квартирном обмене) Несколько семей хотят обменяться квартирами. За один день каждая семья может принять участие не более чем в одном обмене квартирами с какой-нибудь другой семьей. Доказать, что любой сложный обмен можно осуществить не более чем за два дня.

Решение уравнений в подстановках. Чётность и знак перестановок и подстановок. Знак цикла. Задача про «пятнашки»: можно ли, последовательно передвигая фишки на соседнее свободное место, поменять местами фишки 14 и 15, оставив остальные фишки на месте? Можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы угловые кубики одной из граней переставились по кругу, а остальные кубики остались на своих местах (возможно, повернувшись)?

• 3.6бвж, 3.7б, 3.8, 3.11, 3.18, 3.22;
• можно ли, вращая слои куба Рубика на шарнирах, добиться того, чтобы один из боковых кубиков в нём перевернулся, а остальные остались на своих местах, не изменив положения?
• решить уравнения в подстановках:
  • 

Определители квадратных матриц, их вычисление по развёрнутой формуле. Свойства определителя, его изменение при различных преобразованиях матрицы. Вычисление определителей приведением к треугольному виду.

• 10.4б, 16.2, 11.1гд, 11.4, 13.1бвж, 13.2дежз.

Определитель с углом нулей. Определитель Вандермонда. Разложение определителя по строке и столбцу.

• 14.1бзкм★н, 12.2, 12.3ези.

Трёхдиагональные определители и линейные однородные рекуррентные уравнения 2-го порядка. Определитель произведения матриц.

• 14.1где, 12.4, 4.5, 15.2бвг, 16.19;
• вычислить определитель:
• 

Коллоквиум

1. Решение СЛУ в зависимости от параметра.
2. Нахождение ФСР и размерности пространства решений ОСЛУ (1 вариант); нахождение базиса системы векторов и выражение через него остальных векторов системы (2 вариант).
3. Решение матричного уравнения (1 вариант); нахождение обратной матрицы (2 вариант).
4. Вычисление определителя размера 4×4.
5. Вычисление определителя размера n×n.
6. Вычисление трёхдиагонального определителя (1 вариант); решение уравнения в подстановках (2 вариант).

Вычисления над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, решение алгебраических задач геометрическими методами (пример: уравнение |(z-1+i)/(z+1-i)|=1) и геометрических задач методами алгебры комплексных чисел (пример: доказательство теоремы о том, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон).

Тригонометрическая форма записи комплексных чисел, вычисления над комплексными числами в тригонометрической форме. Выражение тригонометрических функций кратных углов через функции исходного угла и степеней тригонометрических функций через функции кратных углов в первой степени с помощью комплексных чисел.

• 20.1еж, 21.2бж, 21.9аг, 21.10, 21.12, 21.13г;
• доказать с помощью комплексных чисел теорему Птолемея: произведение диагоналей четырёхугольника, вписанного в окружность, равно сумме произведений его противоположных сторон.

Извлечение корней из комплексных чисел. Корни из 1, сумма и произведение всех корней степени n из 1. Вычисление сумм с помощью комплексных чисел.

• 22.7еипр, 22.8а, 22.9а, 22.17аб, 22.22★, 23.1вг, 23.2аг.

Многочлены от одной переменной над полем: деление с остатком, теорема Безу, схема Горнера. Разложение многочлена по степеням линейного двучлена, значения высших производных и кратность корня многочлена, формула Тейлора.

• 25.1б, 26.1бв, 26.2бв, 26.3бв, 26.4, 26.6, 26.7аб, 26.11★.

Разложение многочленов на неприводимые множители. Наибольший общий делитель (НОД) многочленов и алгоритм Евклида. Линейное выражение НОД через исходные многочлены: НОД(f,g)=uf+vg, его единственность при ограничениях на степени u и v, и его нахождение методом неопределённых коэффициентов. Избавление от кратных неприводимых множителей в разложении многочлена.

• 25.2вг, 25.3б, 25.5б, 25.7б, 25.8б;
• найти НОД многочленов xⁿ-1 и x^m-1.

Разложение многочленов на неприводимые множители над полями C и R. Неприводимых многочленов над любым полем бесконечно много. Существование неприводимых многочленов сколь угодно большой степени над конечным полем. Алгоритм нахождения всех неприводимых многочленов степени ≤n над конечным полем. Нахождение всех неприводимых многочленов степени ≤4 над полем Z₂.

• 27.1ад, 27.2бгде, 27.6, 27.7, 27.12, 27.14★;
• найти все неприводимые многочлены степени 5 над полем Z₂;
• найти все неприводимые многочлены степени ≤3 со старшим коэффициентом 1 над полем Z₃;
• найти количество неприводимых многочленов степени 4 со старшим коэффициентом 1 над полем Z₃.

Рациональные корни многочлена с целыми или рациональными коэффициентами. Редукция многочленов с целыми коэффициентами по простому модулю, её свойства. Примитивные многочлены, лемма Гаусса. Разложимость многочлена с целыми коэффициентами на множители меньшей степени в Q[x] равносильна разложимости на множители меньшей степени в Z[x]. Разложение многочленов на множители над Q с помощью редукций.

Рациональные дроби: представление в виде суммы многочлена и правильной дроби, разложение правильной дроби в сумму простейших дробей методом неопределённых коэффициентов, случай полей C и R.

• 28.1в, 28.2бвж, 28.8, 28.9, 29.1бе, 29.2аги, 29.3;
• разложить на неприводимые множители над Q:
  • 3x⁵-2x⁴+5x³-4x²-5x-1,
  • 2x⁴-3x³+5x²+8x-5,
  • 3x⁴-x³+5x²+8x-7;
• ★ доказать, что многочлен x⁴-10x²+1 неприводим над Q, но его редукция по любому простому модулю p приводима над Z_p.

Многочлены от нескольких переменных, степень одночлена и многочлена, однородные компоненты многочлена. Лексикографический порядок на одночленах, старший член многочлена, старший член произведения многочленов. Симметрические многочлены: основная теорема, метод неопределённых коэффициентов для нахождения выражения произвольного симметрического многочлена через элементарные. Выражение степенных сумм s₁, s₂, s₃, s₄ через элементарные симметрические многочлены. Теорема Виета. Решение симметрических систем алгебраических уравнений.

• 31.2, 31.5, 31.9авер, 31.15★, 31.21а, 31.25.