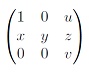Кафедра высшей алгебры

Преподаватель: Д.А. Тимашёв

Занятия проходят по пятницам на 4-й паре (15:00-16:35) в ауд. 454.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И. Кострикина, новое изд., Москва, МЦНМО, 2009. Дополнительные задачи помечены знаком ★.

Единственность нейтрального и обратного элементов в группе. Задание конечных групп таблицей умножения, примеры: группа Клейна V_4, группа кватернионов Q_8. Примеры изоморфных и неизоморфных групп: аддитивная и мультипликативная группы поля R, а также группа положительных вещественных чисел по умножению; Z_4 и V_4; GL_2(C) и GL_3(C). Сопряжённость элементов в группе. Порядок элемента группы, его свойства, циклические группы. Теорема Лагранжа, группы простого порядка. Классификация конечных групп порядка ≤10 (формулировка).

• 55.25абг, 55.26, 56.7в, 56.10, 56.15аге, 55.16, 56.28;
• доказать, что множество G с ассоциативной операцией, в котором есть правая единица (элемент e со свойством g·e=g, ∀g∈G) и правый обратный для каждого g∈G (элемент g' со свойством g·g'=e), является группой;
• какие из групп изоморфны: аддитивная группа поля рациональных чисел, его мультипликтивная группа, группа положительных рациональных чисел (по умножению)?
• доказать, что любая группа порядка 4 изоморфна либо Z_4 либо V_4;
• ★ доказать, что любая группа порядка 6 изоморфна либо Z_6 либо S_3.

Сопряжённость элементов в группе, классы сопряжённости, центр группы. Вычисление классов сопряженности и центра для групп Q_8, S_n, D_n.

• 57.29, 57.30б, 57.36, 58.20б, 58.23, 58.24агж.

Сопряжённость в группе A_n. Нормальные подгруппы в группах S_3, S_4. Вычисление факторгрупп непосредственно и с помощью основной теоремы о гомоморфизмах.

• 58.3, 58.4б, 58.10★, 58.11а, 58.32де, 58.33ге.

Автоморфизмы групп, примеры: Aut(Aut(Aut Z_9)), Aut S_3. Прямое произведение (прямая сумма) групп, примеры разложений и неразложимости групп в прямые произведения (прямые суммы).

• 57.39а, 57.40б, 57.41б, 57.43★, 57.44★, 58.43, 60.2бвг, 60.5ав, 60.7, 60.8б.

Конечно порождённые и не конечно порождённые абелевы группы, примеры. Структура конечно порождённых абелевых групп, её определение, исходя из представления группы в виде факторгруппы свободной группы по подгруппе, заданной набором порождающих элементов, приведением целочисленной матрицы координат порождающих элементов подгруппы к «диагональному» виду. Вычисление порядка элемента в конечно порождённой абелевой группе, представленной как факторгруппа свободной группы. Критерий конечности факторгруппы свободной абелевой группы.

• 60.32, 60.50, 60.52агд, 60.53, 60.54;
• Являются ли конечно порождёнными следующие группы:
  1. группа рациональных дробей m/n, у которых простые делители n содержатся среди {p_1,…,p_s}, с операцией сложения;
  2. группа рациональных дробей m/n≠0, у которых простые делители m и n содержатся среди {p_1,…,p_s}, с операцией умножения;
• доказать две формулы для объёма целочисленного n-мерного параллелепипеда П:
  1. vol(П) = число целых точек в П, не лежащих на его гранях, не содержащих данную вершину 0;
  2. vol(П) = ∑ (1/2^k)⋅(число целых точек внутри всех (n-k)-мерных граней П), где суммирование ведётся по k=0,1,…,n;
• доказать формулу Пика для площади целочисленного многоугольника P:
• S(P) = (число целых точек внутри P)+½⋅(число целых точек на периметре P)-1.

Конечные абелевы группы, их структура, тип группы. Классификация конечных абелевых групп заданного порядка. Определение типа факторгруппы конечной (или конечно порождённой) абелевой группы. Вложимость конечных абелевых групп друг в друга.

• 60.39ежз, 60.40ав, 60.42, 60.43а, 60.45.

Количество подгрупп заданного порядка в данной конечной абелевой группе. Действия групп на множествах, описание орбит и стабилизаторов. Пять правильных многогранников (платоновы тела), двойственность между ними. Группы движений двойственных многогранников совпадают. Группа вращений тетраэдра.

• 60.43бв, 57.1абв, 57.3, 57.9бв, 57.12в, 57.13ав★, 58.36, 58.37.

Теоретико-групповое определение и классификация правильных многогранников. Формула Бернсайда для числа орбит действия конечной группы на конечном множестве. Действие группы на себе сопряжениями: классы сопряжённости и централизаторы, число элементов в классе сопряжённости, формула классов.

• 57.23б, 57.25, 57.31, 58.44;
• сколько существует различных игральных костей? (игральная кость — это кубик, на каждой грани которого написана цифра от 1 до 6, причём цифры могут повторяться);
• доказать формулу Эйлера для правильного многогранника с помощью формулы Бернсайда, рассмотрев действие группы вращений многогранника на множестве точек описанной сферы с нетривиальным стабилизатором.

Коммутант группы, его свойства. Вычисление коммутанта группы G методом оценки сверху (ядро гомоморфизма G в абелеву группу) и снизу (подгруппа, порождённая некоторым количеством коммутаторов). Кратные коммутанты, разрешимые группы, критерий разрешимости (в терминах подгруппы и факторгруппы).

• 62.7г, 62.8б, 62.11в, 62.13, 62.15, 58.38;
• доказать, что -E не является коммутатором в группе SL_2(R);
• вычислить производный ряд для группы, состоящей из невырожденных действительных матриц вида
• 

Силовские подгруппы, теоремы Силова.

• 59.1, 59.3, 59.4, 59.8, 59.13, 59.14.

Коллоквиум

Полупрямые произведения групп, примеры: разложения S_n и D_n в полупрямое произведение. Арифметика конечных групп: доказательство непростоты и разрешимости групп заданного порядка (80, 12).

• 59.22ав, 59.24, 62.18авгде★, 62.22★, 62.23★;
• какие из групп в 60.2бг можно разложить в полупрямое произедение?
• разложить GL_n(K) в полупрямое произведение.

Арифметика конечных групп: доказательство коммутативности групп заданного порядка (455), классификация групп порядка ≤10.

Линейные и матричные представления групп, в том числе представление в пространстве функций на множестве с действием группы. Приводимые и вполне приводимые представления, разложение в прямую сумму неприводимых представлений. Нахождение инвариантных подпространств и доказательство неприводимости (пример: мономиальное представление группы A_n при n≥5). Теорема Машке. Описание неприводимых комплексных представлений конечных абелевых групп (пример: V_4).

• 59.20вг, 69.2, 69.7, 69.9, 69.11, 70.2жз, 70.10;
• доказать, что любая неабелева группа порядка 8 изоморфна либо Q_8, либо D_4;
• разложить мономиальное представление группы A_n при n=3,4 над полем C на неприводимые слагаемые.

Описание одномерных комплексных представлений конечных групп (пример: S_3×D_5). Факты о количестве и размерностях неприводимых комплексных представлений конечной группы. Описание всех неприводимых комплексных представлений группы D_n.

Структурные константы алгебры. Классификация двумерных комплексных алгебр с единицей.

• 70.34бге, 70.37б, 70.39, 63.21б, 63.22а;
• описать все одномерные комплексные представления группы A_4×D_4;
• описать все неприводимые комплексные представления групп Q_8 и A_4×Z_3.

Идеалы, главные идеалы, кольца главных идеалов. Факторалгебры K[x]/(f), их свойства, вычисления в K[x]/(f). Присоединение корня, избавление от иррациональности в знаменателе. Минимальный многочлен.

• 64.8б, 64.2а, 64.43, 67.3бгдеж, 67.12;
• представить выражение (a²-3a-1)/(a²+2a+1) в виде многочлена от a наименьшей возможной степени с рациональными коэффициентами, где a∈C — корень многочлена x³+x²+3x+4.

1. Вычисление факторгруппы свободной абелевой группы и нахождение в ней количества элементов заданного порядка (1 вариант) и порядка заданного элемента (2 вариант).
2. Описание орбит действия группы на множестве (1 вариант); нахождение централизатора элемента группы подстановок и количества элементов в его классе сопряжённости (2 вариант).
3. Описание силовских подгрупп в группе (1 вариант); доказательство коммутативности группы заданного порядка (2 вариант).
4. Доказательство разрешимости группы заданного порядка (1 вариант); вычисление производного ряда группы (2 вариант).
5. Описание одномерных комплексных представлений группы.
6. Избавление от иррациональности в знаменателе выражения в поле, получаемом присоединением корня неприводимого многочлена к полю Z_3 (1 вариант) и C (2 вариант).